题目内容
1．
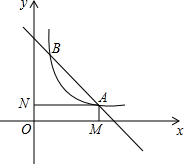函数y=6-x与函数y=$\frac{4}{x}$交于A、B两点，过点A作x轴与y轴的垂线，垂足分别为M、N，则四边形OMAN的面积和周长分别为多少？
分析 根据反比例函数k的几何意义即可求出四边形OMAN的值，然后联立解析式求出点A的坐标，即可求出四边形OMAN的周长．
解答 解：由于点A在反比例函数的图象上，
∴四边形OMAN的面积为：4
联立$\left\{\begin{array}{l}{y=6-x}\\{y=\frac{4}{x}}\end{array}\right.$
解得：x=3±$\sqrt{5}$，
∴令x=3+$\sqrt{5}$代入y=6-x，
∴y=3-$\sqrt{5}$，
∴周长为：2（3+$\sqrt{5}$+3-$\sqrt{5}$）=12，
点评 本题考查反比例函数与一次函数的交点问题，解题的关键是联立方程组求出交点A，本题属于中等题型．
练习册系列答案
一线名师提优试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
11．有下列各数：0.01，10，-$\frac{1}{3}$，-|-2|，-90，-（-3.5），其中属于负数的共有（ ）
| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
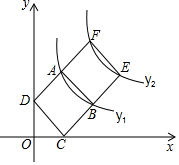如图，在边长均为1的正方形ABCD和ABEF中，顶点A，B在双曲线y1=$\frac{{k}_{1}}{x}$（k1≠0）上，顶点E，F在双曲线y2=$\frac{{k}_{2}}{x}$（k2≠0）上，顶点C，D分别在x轴和y轴上，则k1=1，k2=3．
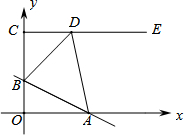如图，在平面直角坐标系中，点C（0，4），射线CE∥x轴，直线y=-$\frac{1}{2}$x+b交线段OC于点B，交x轴于点A，D是射线CE上一点．若存在点D，使得△ABD恰为等腰直角三角形，则b的值为$\frac{4}{3}$或$\frac{8}{3}$或2．
如图，四边形ABCD中，AD=2AB，E是AD的中点，AC平分∠BAD，连接CE．求证：CB=CE．
父亲节这天，小明送给父亲一个礼盒（如图），该礼盒的主视图是（ ）
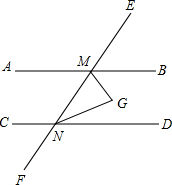如图，AB∥CD，∠BMN与∠DNM的平分线相交于点G，