题目内容
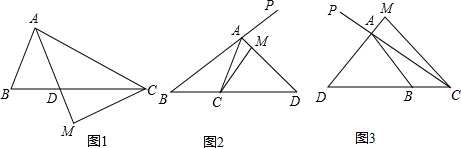
11.已知,在△ABC中,AD为△ABC的角平分线或外角平分线,交BC边所在的直线于点D,过点C作CM⊥AD于点M,已知AB=AD.(1)当AD为△ABC的角平分线(如图1),求证:AC-AB=2DM;
(2)当AD为△ABC的角平分线(如图2,3),其它条件不变,请分别写出线段AC、AB、DM之间的数量关系;
(3)当AD为△ABC的角平分线(如图3),请证明线段AC、AB、DM之间的数量关系.
分析 (1)如图1,延长CM、AB交于点G,作MN∥AG交BC于点N.只要证明AG=AC、DM=MN,MN是△BCG的中位线即可解决问题;
(2)如图2,结论:AB+AC=2DM.如图3,结论:AB+AC=2DM.延长CM、BA交于点G,作MN∥AB交BC于点N,即可得出结论;
(3)如图3,延长CM、BA交于点G,作MN∥AB交BC于点N,根据三角形中位线定理进行证明即可.
解答 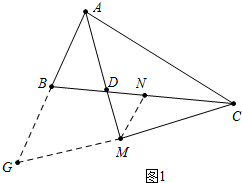 解:(1)证明:如图1,延长CM、AB交于点G,作MN∥AG交BC于点N.
解:(1)证明:如图1,延长CM、AB交于点G,作MN∥AG交BC于点N.
∵AM⊥CG,
∴∠AMG=∠AMC=90°,
∴∠G+∠GAM=90°,∠ACM+∠CAM=90°,
∵∠GAM=∠CAM,
∴∠G=∠ACM,
∴AC=AG,
∵AM⊥CG,
∴GM=MC,
∵MN∥BG,
∴BN=NC,
∴MN=$\frac{1}{2}$BG,即BG=2MN,
∵AB=AD,
∴∠ABD=∠ADB,
∵∠ABD=∠MND,∠ADB=∠MDN,
∴∠MND=∠MDN,
∴DM=MN,
∴BG=2DM.
∵AC-AB=AG+AB=BG,
∴AC-AB=2DM.
(2)图2中,线段AC、AB、DM之间的数量关系为:AB+AC=2DM.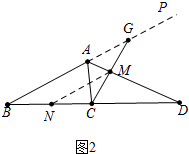 图3中,线段AC、AB、DM之间的数量关系为:AB+AC=2DM.
图3中,线段AC、AB、DM之间的数量关系为:AB+AC=2DM.
理由:如图2,延长CM、BA交于点G,作MN∥AB交BC于点N.
∵AM⊥CG,
∴∠AMG=∠AMC=90°,
∴∠AGM+∠GAM=90°,∠ACM+∠CAM=90°
∵∠GAM=∠CAM,
∴∠AGM=∠ACM,
∴AC=AG,
∵AM⊥CG,
∴GM=MC,
∵MN∥BG,
∴BN=NC,
∴MN=$\frac{1}{2}$BG,即BG=2MN,
∵AB=AD,
∴∠ABD=∠D,
∵∠ABD=∠MND,
∴∠MND=∠MDN,
∴DM=MN,
∴BG=2DM.
∵AC+AB=AG+AB=BG,
∴AC+AB=2DM.
(3)如图3,结论为:AB+AC=2DM.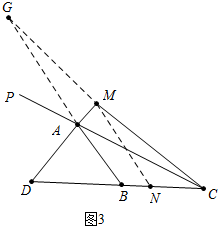
证明:延长CM、BA交于点G,作MN∥AB交BC于点N.
∵AM⊥CG,
∴∠AMG=∠AMC=90°,
∴∠G+∠GAM=90°,∠ACM+∠CAM=90°
∵∠DAB=∠DAP,∠DAB=∠GAM,∠DAP=∠CAM,
∴∠GAM=∠CAM,
∴∠AGM=∠ACM,
∴AC=AG,
∵AM⊥CG,
∴GM=MC,
∵MN∥BG,
∴BN=NC,
∴MN=$\frac{1}{2}$BG,即BG=2MN,
∵AB=AD,
∴∠ABD=∠D,
∵∠ABD=∠MND,
∴∠MND=∠MDN,
∴DM=MN,
∴BG=2DM.
∵AC+AB=AG+AB=BG,
∴AC+AB=2DM.
点评 本题属于三角形综合题,主要考查了三角形中位线定理、等腰三角形的判定和性质、平行线性质,平行线等分线段定理等知识的综合应用,解题的关键是学会添加常用辅助线,利用三角形中位线定理解决问题.解题时注意:三角形的中位线平行于第三边,并且等于第三边的一半.

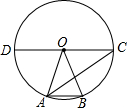 如图,在⊙O中,CD是直径,点A,点B在⊙O上,连接OA、OB、AC、AB,若∠AOB=40°,CD∥AB,则∠BAC的大小为( )
如图,在⊙O中,CD是直径,点A,点B在⊙O上,连接OA、OB、AC、AB,若∠AOB=40°,CD∥AB,则∠BAC的大小为( )| A. | 30° | B. | 35° | C. | 40° | D. | 70° |
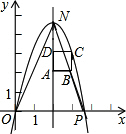 如图,在直角坐标系中,点P的坐标是(n,0)(n>0),抛物线y=-x2+bx+c经过原点O和点P,已知正方形ABCD的三个顶点为A(2,2),B(3,2),D(2,3).
如图,在直角坐标系中,点P的坐标是(n,0)(n>0),抛物线y=-x2+bx+c经过原点O和点P,已知正方形ABCD的三个顶点为A(2,2),B(3,2),D(2,3).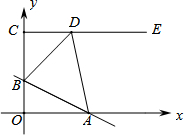 如图,在平面直角坐标系中,点C(0,4),射线CE∥x轴,直线y=-$\frac{1}{2}$x+b交线段OC于点B,交x轴于点A,D是射线CE上一点.若存在点D,使得△ABD恰为等腰直角三角形,则b的值为$\frac{4}{3}$或$\frac{8}{3}$或2.
如图,在平面直角坐标系中,点C(0,4),射线CE∥x轴,直线y=-$\frac{1}{2}$x+b交线段OC于点B,交x轴于点A,D是射线CE上一点.若存在点D,使得△ABD恰为等腰直角三角形,则b的值为$\frac{4}{3}$或$\frac{8}{3}$或2.