题目内容
4. 如图,在直线y=kx+b交坐标轴于A(-3.0)、B(0,5)两点,则不等式kx+b<5的解集为( )
如图,在直线y=kx+b交坐标轴于A(-3.0)、B(0,5)两点,则不等式kx+b<5的解集为( )| A. | x>-3 | B. | x<-3 | C. | x>0 | D. | x<0 |
分析 不等式kx+b<5的解集,就是求函数值小于5时,x的取值范围.
解答 解:从图象上可以看出当y<5时,x<0,
即不等式kx+b<5的解集为x<0.
故选:D.
点评 本题考查一次函数的性质,解题时应结合函数和不等式的关系找出正确的答案.

练习册系列答案
相关题目
12. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论:
①2a+b=0;②b+2c<0;③4a+2b+c<0;④若(0,y1),($\frac{3}{2}$,y2)是抛物线上的两点,那么y1<y2.其中正确的是( )
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论:①2a+b=0;②b+2c<0;③4a+2b+c<0;④若(0,y1),($\frac{3}{2}$,y2)是抛物线上的两点,那么y1<y2.其中正确的是( )
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
19.已知二次函数y=x2-(m-1)x-m,其中m>0,它的图象与x轴从左到右交于R和Q两点,与y轴交于点P,点O是坐标原点.下列判断中不正确的是( )
| A. | 方程x2-(m-1)x-m=0一定有两个不相等的实数根 | |
| B. | 点R的坐标一定是(-1,0) | |
| C. | △POQ是等腰直角三角形 | |
| D. | 该二次函数图象的对称轴在直线x=-1的左側 |
9. 已知y是x的函数,自变量x的取值范围x>0,下表是y与x的几组对应值:
已知y是x的函数,自变量x的取值范围x>0,下表是y与x的几组对应值:
小腾根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小腾的探究过程,请补充完整:
(1)如图,在平面直角坐标系xOy中,描出了以上表格中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(2)根据画出的函数图象,写出:
①x=4对应的函数值y约为2;
②该函数的一条性质:该函数有最大值.
 已知y是x的函数,自变量x的取值范围x>0,下表是y与x的几组对应值:
已知y是x的函数,自变量x的取值范围x>0,下表是y与x的几组对应值:| x | … | 1 | 2 | 3 | 5 | 7 | 9 | … |
| y | … | 1.98 | 3.95 | 2.63 | 1.58 | 1.13 | 0.88 | … |
下面是小腾的探究过程,请补充完整:
(1)如图,在平面直角坐标系xOy中,描出了以上表格中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(2)根据画出的函数图象,写出:
①x=4对应的函数值y约为2;
②该函数的一条性质:该函数有最大值.
16.在平面直角坐标系中,点(a-3,2a+1)在第二象限内,则a的取值范围是( )
| A. | -3<a<$\frac{1}{2}$ | B. | $\frac{1}{2}$<a<3 | C. | -3<a<-$\frac{1}{2}$ | D. | $-\frac{1}{2}$<a<3 |
13. 数学课上探究一次函数图象与反比例函数图象有交点时的相关结论:已知直线y=kx+b与x轴、y轴分别交于点C(x,0)、D(0,y),与双曲线y=$\frac{m}{x}$交于点A(x1,y1),B(x2,y2).
数学课上探究一次函数图象与反比例函数图象有交点时的相关结论:已知直线y=kx+b与x轴、y轴分别交于点C(x,0)、D(0,y),与双曲线y=$\frac{m}{x}$交于点A(x1,y1),B(x2,y2).
(1)填空与观察:
(2)发现与验证:
数学学习小组在探究图象交点时发现以下结论:
①x1+x2=x;②y1+y2=y;③当b2+4mk≥0时,两函数图象一定会相交.
你认为以上探究的结论中正确的有①②③(填序号),请选择一个加以证明.
(3)应用与拓展:
连接AO,BO,判断△ACO与△BOD的面积有什么关系,并说明理由.
 数学课上探究一次函数图象与反比例函数图象有交点时的相关结论:已知直线y=kx+b与x轴、y轴分别交于点C(x,0)、D(0,y),与双曲线y=$\frac{m}{x}$交于点A(x1,y1),B(x2,y2).
数学课上探究一次函数图象与反比例函数图象有交点时的相关结论:已知直线y=kx+b与x轴、y轴分别交于点C(x,0)、D(0,y),与双曲线y=$\frac{m}{x}$交于点A(x1,y1),B(x2,y2).(1)填空与观察:
| 函数关系式 | C(x,0) | D(0,y) | A (x1,y1) | B(x2,y2) |
| y=2x+2,y=$\frac{4}{x}$,如图1 | (-1,0) | (0,2) | (1 , 4) | (-2,-2) |
| y=x-3,y=$\frac{10}{x}$,如图2 | (3,0) | (0,-3) | (5,2) | ( -2, -5) |
数学学习小组在探究图象交点时发现以下结论:
①x1+x2=x;②y1+y2=y;③当b2+4mk≥0时,两函数图象一定会相交.
你认为以上探究的结论中正确的有①②③(填序号),请选择一个加以证明.
(3)应用与拓展:
连接AO,BO,判断△ACO与△BOD的面积有什么关系,并说明理由.
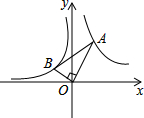 如图,已知第一象限内的点A在反比例函数y=$\frac{2}{x}$上,第二象限的点B在反比例函数y=$\frac{k}{x}$上,且OA⊥OB,tanA=$\frac{1}{3}$,则k的值为-$\frac{2}{9}$.
如图,已知第一象限内的点A在反比例函数y=$\frac{2}{x}$上,第二象限的点B在反比例函数y=$\frac{k}{x}$上,且OA⊥OB,tanA=$\frac{1}{3}$,则k的值为-$\frac{2}{9}$.