题目内容
15.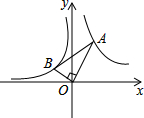 如图,已知第一象限内的点A在反比例函数y=$\frac{2}{x}$上,第二象限的点B在反比例函数y=$\frac{k}{x}$上,且OA⊥OB,tanA=$\frac{1}{3}$,则k的值为-$\frac{2}{9}$.
如图,已知第一象限内的点A在反比例函数y=$\frac{2}{x}$上,第二象限的点B在反比例函数y=$\frac{k}{x}$上,且OA⊥OB,tanA=$\frac{1}{3}$,则k的值为-$\frac{2}{9}$.
分析 作AC⊥x轴于点C,作BD⊥x轴于点D,易证△OBD∽△AOC,则面积的比等于相似比的平方,即tanA的平方,然后根据反比例函数中比例系数k的几何意义即可求解.
解答 解:作AC⊥x轴于点C,作BD⊥x轴于点D.
则∠BDO=∠ACO=90°,
则∠BOD+∠OBD=90°,
∵OA⊥OB,
∴∠BOD+∠AOC=90°,
∴∠BOD=∠AOC,
∴△OBD∽△AOC,
∴$\frac{S△OBD}{S△AOC}$=($\frac{OB}{OA}$)2=(tanA)2=$\frac{1}{9}$,
又∵S△AOC=$\frac{1}{2}$×2=1,
∴S△OBD=$\frac{1}{9}$,
∴k=-$\frac{2}{9}$.
故答案为:-$\frac{2}{9}$.
点评 本题考查了相似三角形的判定与性质,以及反比例函数的比例系数k的几何意义,正确作出辅助线求得两个三角形的面积的比是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.下列说法正确的是( )
| A. | 相等的圆心角所对的弧相等 | |
| B. | 正n边形既是轴对称图形,也是中心对称图形 | |
| C. | 顺次连接一个四边形各边中点所得的四边形是平行四边形 | |
| D. | 圆周角的度数等于圆心角度数的一半 |
10.直角三角形两个锐角∠A与∠B的函数关系是( )
| A. | 正比例函数 | B. | 一次函数 | C. | 反比例函数 | D. | 二次函数 |
20.已知函数y=(3-m)x+m-1的图象过第一、二、四象限,则m的取值范围是( )
| A. | m>3 | B. | m<1 | C. | 不存在 | D. | 1<m<3 |
4. 如图,在直线y=kx+b交坐标轴于A(-3.0)、B(0,5)两点,则不等式kx+b<5的解集为( )
如图,在直线y=kx+b交坐标轴于A(-3.0)、B(0,5)两点,则不等式kx+b<5的解集为( )
 如图,在直线y=kx+b交坐标轴于A(-3.0)、B(0,5)两点,则不等式kx+b<5的解集为( )
如图,在直线y=kx+b交坐标轴于A(-3.0)、B(0,5)两点,则不等式kx+b<5的解集为( )| A. | x>-3 | B. | x<-3 | C. | x>0 | D. | x<0 |
 综合与探究:如图,已知抛物线y=-x2+2x+3的图象与x轴交于点A,B(A在B的右侧),与y轴交于点C,对称轴与抛物线交于点D,与x轴交于点E.
综合与探究:如图,已知抛物线y=-x2+2x+3的图象与x轴交于点A,B(A在B的右侧),与y轴交于点C,对称轴与抛物线交于点D,与x轴交于点E. 如图,AB是半圆O的直径,过点O作弦AD的垂线交半圆O于点E,交AC于点C,使∠BED=∠C.
如图,AB是半圆O的直径,过点O作弦AD的垂线交半圆O于点E,交AC于点C,使∠BED=∠C.