题目内容
 如图,在平面直角坐标系中,?ABCD,顶点A(1,b),B(3,b),D(2,b+1)
如图,在平面直角坐标系中,?ABCD,顶点A(1,b),B(3,b),D(2,b+1)(1)点C的坐标是
(2)双曲线y=
| k |
| x |
(3)如果?ABCD与双曲线y=
| 4 |
| x |
考点:反比例函数综合题
专题:综合题
分析:(1)由ABCD为平行四边形,得到DC与AB平行,且DC=AB,即C与D纵坐标相同,横坐标相差2,得出C坐标即可;
(2)根据B与D在反比例图象上,得到C与D横纵坐标乘积相等,求出b的值确定出B坐标,进而求出k的值,确定出双曲线解析式;
(3)抓住两个关键点,将A坐标代入双曲线解析式求出b的值;将C坐标代入双曲线解析式求出b的值,即可确定出平行四边形与双曲线总有公共点时b的范围.
(2)根据B与D在反比例图象上,得到C与D横纵坐标乘积相等,求出b的值确定出B坐标,进而求出k的值,确定出双曲线解析式;
(3)抓住两个关键点,将A坐标代入双曲线解析式求出b的值;将C坐标代入双曲线解析式求出b的值,即可确定出平行四边形与双曲线总有公共点时b的范围.
解答:解:(1)根据题意得:C(4,b+1);
故答案为:(4,b+1);
(2)∵双曲线y=
过?ABCD的顶点B(3,b)和D(2,b+1),
∴3b=2(b+1),
解得:b=2,即B(3,2),D(2,3),
则该双曲线解析式为y=
;
(3)将A(1,b)代入y=
得:b=4;将C(4,b+1)代入y=
得:b+1=1,即b=0,
则?ABCD与双曲线y=
(x>0)总有公共点时,b的取值范围为0≤b≤4.
故答案为:(4,b+1);
(2)∵双曲线y=
| k |
| x |
∴3b=2(b+1),
解得:b=2,即B(3,2),D(2,3),
则该双曲线解析式为y=
| 6 |
| x |
(3)将A(1,b)代入y=
| 4 |
| x |
| 4 |
| x |
则?ABCD与双曲线y=
| 4 |
| x |
点评:此题属于反比例函数综合题,涉及的知识有:待定系数法确定反比例解析式,平行四边形的性质,以及反比例函数的图象与性质,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
 按图1中所示程序进行计算:
按图1中所示程序进行计算: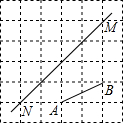 如图,在每个小正方形的边长均为1个单位长度的方格纸中,有线段AB和直线MN,点A、B、M、N均在小正方形的顶点上.
如图,在每个小正方形的边长均为1个单位长度的方格纸中,有线段AB和直线MN,点A、B、M、N均在小正方形的顶点上. 货轮在海上以每小时40海里的速度沿南偏东40°的方向航行,已知货轮在B处时,测得灯塔A在其北偏东80°的方向上,航行半小时后货轮到达C处,此时测到灯塔A在其北偏东20°的方向上,求货轮到达C处时与灯塔A的距离.
货轮在海上以每小时40海里的速度沿南偏东40°的方向航行,已知货轮在B处时,测得灯塔A在其北偏东80°的方向上,航行半小时后货轮到达C处,此时测到灯塔A在其北偏东20°的方向上,求货轮到达C处时与灯塔A的距离.