题目内容
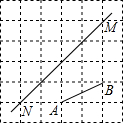如图，在每个小正方形的边长均为1个单位长度的方格纸中，有线段AB和直线MN，点A、B、M、N均在小正方形的顶点上．（1）在方格纸中画四边形ABCD（四边形的各顶点均在小正方形的顶点上），使四边形ABCD是以直线MN为对称轴的轴对称图形，点A的对称点为点D，点B的对称点为点C；
（2）若直线MN上存在点P，使得PA+PB的值最小，请直接写出PA的长度．
考点：利用轴对称设计图案,轴对称-最短路线问题
专题：
分析：（1）利用网格求出对称点进而得出符合题意的图形；
（2）利用轴对称最短路线求法结合相似三角形的判定与性质得出AP的长即可．
（2）利用轴对称最短路线求法结合相似三角形的判定与性质得出AP的长即可．
解答：解：（1）如图所示：
；
（2）如图所示：连接AC，交MN于点P，
∵AD∥BC，
∴△APF∽△CPE，
∴
=
=
，
EF为梯形ABCD的高，则EF=
，
可得AF=
，CE=
，
=
，
解得：AP=
．
；（2）如图所示：连接AC，交MN于点P，
∵AD∥BC，
∴△APF∽△CPE，
∴
| AF |
| CE |
| AP |
| PC |
| FP |
| PE |
EF为梯形ABCD的高，则EF=
3
| ||
| 2 |
可得AF=
| 2 |
3
| ||
| 2 |
| 2 |
| 3 |
| AP | ||||
|
解得：AP=
3
| ||
| 5 |
点评：此题主要考查了利用轴对称设计图案以及相似三角形的判定与性质和勾股定理等知识，得出EF的长是解题关键．
练习册系列答案
相关题目
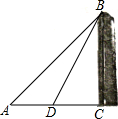津塔在天津大沽桥旁，是一座位于海河河畔的摩天大楼，某校数学兴趣小组要测量津塔的高度．如图，他们在点A处测得津塔的最高点B的仰角为45°，再往津塔方向前进至点D处测得津塔的高点B的仰角为60°，AD=142.6m．根据这个兴趣小组测得的数据，计算津塔的高度CB（
快、慢两车分别从相距360千米的甲乙两地同时出发，匀速行驶，先相向而行，快车到达乙地后，停留1小时，然后安原路原速返回，快车比慢车晚1小时到达甲地，快、慢两车距甲地的路程y（千米）与出发后所用的时间x（小时）之间的关系如图，请结合图象信息解答下列问题：
△ABC在直角坐标系内的位置如图．
如图，△ABC中，∠ABC=∠ACB=45°，直线l经过A点，BD⊥l，CE⊥l，垂足分别为D、E，先证明△BDA≌△AEC，然后直接写出BD、DE、EC之间的数量关系．
如图，在平面直角坐标系中，?ABCD，顶点A（1，b），B（3，b），D（2，b+1）