题目内容
20. 如图,在正方形ABCD中,E、F分别是边BC、CD上的点,∠EAF=45°,正方形ABCD的边长为3,则△ECF的周长为6.
如图,在正方形ABCD中,E、F分别是边BC、CD上的点,∠EAF=45°,正方形ABCD的边长为3,则△ECF的周长为6.
分析 通过作辅助线,证明△ABF′≌△ADF和△EAF′≌△EAF,求出EF=DF+BE,三角形的周长=三边之和,由三角形的全等,通过等量代换,得出BE+BF′=EF′.
解答 证明:延长CB到F′,使BF′=DF,
在正方形ABCD中,AB=AD,∠ABC=∠D=90°,
∴∠ABF′=180°-∠ABC=90°=∠D,
∵在△ABF′和△ADF中
$\left\{\begin{array}{l}{AB=AD}\\{∠ABF′=∠D}\\{BF′=DF}\end{array}\right.$
∴△ABF′≌△ADF(SAS),
∴AF′=AF,∠1=∠2,
∴∠EAF′=∠1+∠3=∠2+∠3=90°-∠EAF=45°=∠EAF,
在△EAF′和△EAF中
$\left\{\begin{array}{l}{AE=AE}\\{∠EAF′=∠EAF}\\{AF′=AF}\end{array}\right.$
∴△EAF′≌△EAF(SAS),
∴EF′=EF,
∴C△CEF=EC+CF+EF
=EC+CF+EF′
=EC+BE+CF+BF′
=BC+CF+DF
=BC+CD=2AB=6,
故答案为:6.
点评 本题是一道综合题,考查三角形的全等,正方形的性质,以及等量代换的方法和转化的思想,能正确作出辅助线是解此题的关键,难度适中.

练习册系列答案
相关题目
11. 如图是一个正方体的表面展开图,则原正方体中与“我”字所在的面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“我”字所在的面相对的面上标的字是( )
 如图是一个正方体的表面展开图,则原正方体中与“我”字所在的面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“我”字所在的面相对的面上标的字是( )| A. | 美 | B. | 丽 | C. | 包 | D. | 头 |
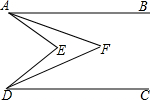 已知:如图,AB∥CD,E,F分别是AB,CD之间的两点,且∠BAF=2∠EAF,∠CDF=2∠EDF.
已知:如图,AB∥CD,E,F分别是AB,CD之间的两点,且∠BAF=2∠EAF,∠CDF=2∠EDF.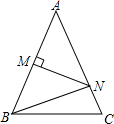 如图,△ABC中,AB=AC,∠A=38°,MN垂直平分AB,则∠BNC=76°.
如图,△ABC中,AB=AC,∠A=38°,MN垂直平分AB,则∠BNC=76°.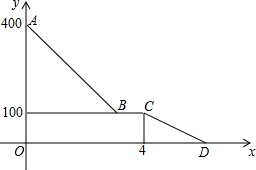 小红驾车从甲地到乙地,设她出发第xh时距离乙地ykm,图中的折线表示她在整个驾车过程中y与x之间的函数关系.
小红驾车从甲地到乙地,设她出发第xh时距离乙地ykm,图中的折线表示她在整个驾车过程中y与x之间的函数关系.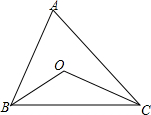 O是△ABC内一点,且BO,CO分别平分∠ABC,∠ACB.
O是△ABC内一点,且BO,CO分别平分∠ABC,∠ACB.