题目内容
10.在一个不透明的布袋里装有4个完全相同的标有数字1、2、3、4的小球.小明从布袋里随机取出一个小球,记下数字为x,小红从布袋里剩下的小球中随机取出一个,记下数字为y.计算由x、y确定的点(x,y)在函数y=-x+5的图象上的概率.分析 首先根据题意画出树状图,然后由树状图求得所有等可能的结果与点(x,y)在函数y=-x+5的图象上的情况,再利用概率公式即可求得答案.
解答 解:画树状图得:
∵共有等可能的结果12种:(x,y)为(1,2)、(1,3)、(1,4)、(2,1)、(2,3)、(2,4)、(3,1)、(3,2)、(3,4)、(4,1)、(4,2)、(4,3);其中(x,y)所表示的点在函数y=-x+5的图象上的有4种,
∴P(点(x,y)在函数y=-x+5的图象上)=$\frac{4}{12}$=$\frac{1}{3}$.
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
1.若函数y=mx2-(m-3)x-4的图象与x轴只有一个交点,则m的值为( )
| A. | 0 | B. | 1或9 | C. | -1或-9 | D. | 0或-1或-9 |
5.下列四个多项式,能因式分解的是( )
| A. | a-1 | B. | a2+1 | C. | x2-4y | D. | x2-6x+9 |
2.某种玉米种子在相同条件下的发芽实验结果如下表:
(1)计算并完成表格;
(2)请估计,当n很大时,频率将接近0.70;
(3)这种玉米种子的发芽概率的估计值是但是多少?请简要说明理由.
| 每批粒数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 发芽的粒数m | 65 | 111 | 136 | 345 | 560 | 700 |
| 发芽的频率$\frac{m}{n}$ | 0.65 | 0.74 | 0.68 | 0.69 |
(2)请估计,当n很大时,频率将接近0.70;
(3)这种玉米种子的发芽概率的估计值是但是多少?请简要说明理由.
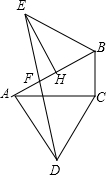 已知:如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,以AC为边作等边△ACD,并作斜边AB的垂直平分线EH,且EB=AB,联结DE交AB于点F,求证:EF=DF.
已知:如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,以AC为边作等边△ACD,并作斜边AB的垂直平分线EH,且EB=AB,联结DE交AB于点F,求证:EF=DF. 如图,在△ABC中,∠C=90°,若BD∥AE,∠DBC=20°,则∠CAE的度数是70°.
如图,在△ABC中,∠C=90°,若BD∥AE,∠DBC=20°,则∠CAE的度数是70°. 如图,在正方形ABCD中,E、F分别是边BC、CD上的点,∠EAF=45°,正方形ABCD的边长为3,则△ECF的周长为6.
如图,在正方形ABCD中,E、F分别是边BC、CD上的点,∠EAF=45°,正方形ABCD的边长为3,则△ECF的周长为6.