题目内容
13．
如图，在矩形ABCD中，连接对角线AC，BD，延长BC至点E，使BC=CE，连接DE．求证：DE=AC．
分析 ①根据矩形对角线相等得：AC=BD，②根据中垂线性质得：BD=DE，③根据等量代换可得结论．
解答 证明：∵四边形ABCD是矩形，
∴AC=BD，∠BCD=90°，
∵BC=CE，
∴DC是BE的中垂线，
∴BD=DE，
∴DE=AC．
点评 本题考查了矩形的性质、中垂线的性质，属于基础题，熟练掌握矩形的性质是关键，其方法有很多，也可以证明四边形ACED是平行四边形得出结论．
练习册系列答案
相关题目
4．
如图，有一块直角三角形纸片，两直角边分别为：AC=6cm，BC=8cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，则CD等于（ ）
如图，有一块直角三角形纸片，两直角边分别为：AC=6cm，BC=8cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，则CD等于（ ）| A． | 2 cm | B． | 3 cm | C． | 4 cm | D． | 5 cm |
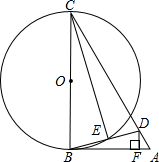如图，在△ABC中，D为AC上一点，且CD=CB，以BC为直径作⊙O，交BD于点E，连接CE，过D作DF⊥AB于点F，∠BCD=2∠ABD．
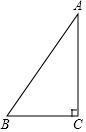如图，在△ABC 中，∠C=90°
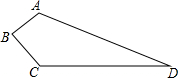某小区有一块四边形空地（如图所示，四边形ABCD），规划在这块空地上种植毎平方米60元的草坪用以美化环境，施工人员测得（单位：米）：AB=3，BC=4，CD=12，DA=13，∠B=90°，求小区种植这种草坪需多少钱？
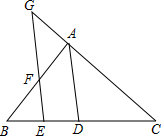如图，在△ABC中，AD平分∠BAC，交BC于点D，点G在CA的延长线上，GE交AB，BC于点F，E，且∠BFE=∠G．
3．在平面直角坐标系中，点（m2+1，1）一定在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |