题目内容
14．
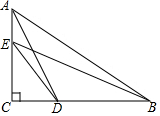如图，在△ABC中，∠C=90°，点D，E分别在边BC，AC上，若DE=$\sqrt{5}$，AB=5，求AD2+BE2的值．
分析 根据勾股定理可得AD2=AC2+CD2，BE2=EC2+BC2，进而可得AD2+BE2=AC2+CD2+EC2+BC2，再根据DE=$\sqrt{5}$，AB=5可得答案．
解答 解：∵在Rt△ACD中，AD2=AC2+CD2，
在Rt△ECB中，BE2=EC2+BC2，
∴AD2+BE2=AC2+CD2+EC2+BC2，
∵AB=5，
∴AC2+BC2=25，
∵DE=$\sqrt{5}$，
∴EC2+CD2=5，
∴AD2+BE2=25+5=30．
点评 此题主要考查了勾股定理的应用，关键是掌握在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．
练习册系列答案
相关题目
5．
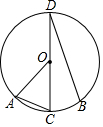如图，CD是圆O的直径，AC，BD是弦，C是弧AB的中点，且∠BDC=25°，则∠AOC的度数是（ ）
如图，CD是圆O的直径，AC，BD是弦，C是弧AB的中点，且∠BDC=25°，则∠AOC的度数是（ ）| A． | 25° | B． | 45° | C． | 50° | D． | 60° |
2．
如图，在△ABC中，点P在边AB上，则在下列四个条件中：：①∠ACP=∠B；②∠APC=∠ACB；③AC2=AP•AB；④AB•CP=AP•CB，能满足△APC与△ACB相似的条件是（ ）
如图，在△ABC中，点P在边AB上，则在下列四个条件中：：①∠ACP=∠B；②∠APC=∠ACB；③AC2=AP•AB；④AB•CP=AP•CB，能满足△APC与△ACB相似的条件是（ ）| A． | ①②④ | B． | ①③④ | C． | ②③④ | D． | ①②③ |
9．下列说法中正确的有（ ）
①过一点有且只有一条直线与已知直线垂直；
②如果两个角相等，那么这两个角是对顶角；
③如果两条直线被第三条直线所截，那么内错角相等；
④联结直线外一点与直线上各点的所有线段，垂线段最短；
⑤邻补角的平分线互相垂直．
①过一点有且只有一条直线与已知直线垂直；
②如果两个角相等，那么这两个角是对顶角；
③如果两条直线被第三条直线所截，那么内错角相等；
④联结直线外一点与直线上各点的所有线段，垂线段最短；
⑤邻补角的平分线互相垂直．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
19．单项式$\frac{4π{x}^{2}{y}^{2}}{9}$的系数与次数分别为（ ）
| A． | $\frac{4}{9}$，7 | B． | $\frac{4}{9}$π，6 | C． | 4π，6 | D． | $\frac{4}{9}$π，4 |
6．下列长度的三条线段能组成三角形的是（ ）
| A． | 1cm 2cm 3cm | B． | 1cm 2cm 3.5cm | C． | 5cm 8cm 12cm | D． | 4cm 5cm 9cm |
3．-$\frac{1}{8}$的相反数是（ ）
| A． | -$\frac{1}{8}$ | B． | -8 | C． | $\frac{1}{8}$ | D． | 8 |
4．
如图，一副三角板（直角顶点重合）摆放在桌面上，若∠AOD=145°，则∠BOC等于（ ）
如图，一副三角板（直角顶点重合）摆放在桌面上，若∠AOD=145°，则∠BOC等于（ ）| A． | 35° | B． | 40° | C． | 45° | D． | 50° |