题目内容
4．从一副扑克牌中取出的两组牌，分别是黑桃1、2、3、4和方块1、2、3、4，将它们背面朝上分别重新洗牌后，从两组牌中各摸出一张，分别用m、n、表示其数字；请你用列举法（列表或画树状图）分析说明：（1）摸出的两张牌的牌面数字之和等于5的概率是多少？
（2）关于x的方程x2+mx+n=0没有实数根的概率是多少？
分析 （1）依据题意先用列表法或画树状图法分析所有等可能的出现结果，然后根据概率公式求出该事件的概率．
（2）由方程x2+mx+n=0没有实数根．可知根的判别式小于零，进而可求出m和n的大小关系，结合（1）即可求出其概率．
解答 解：
（1）可以用下表列举所有可能得到的牌面数字之和：
| 1 | 2 | 3 | 4 | |
| 1 | （1，1） | （2，1） | （3，1） | （4，1） |
| 2 | （1，2） | （2，2） | （3，2） | （4，2） |
| 3 | （1，3） | （2，3） | （3，3） | （4，3） |
| 4 | （1，4） | （2，4） | （3，4） | （4，4） |
（2）∵方程x2+mx+n=0没有实数根，
∴△＜0，
∴m2-4n＜0，
即m2＜4n，
由（1）可知符合题意的情况共有8种，所以方程x2+mx+n=0没有实数根的概率=$\frac{8}{16}$=$\frac{1}{2}$．
点评 此题考查了列举法与树状图法以及根的判别式的运用，用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
15．下列计算正确的是（ ）
| A． | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B． | $\sqrt{2}$•$\sqrt{3}$=$\sqrt{6}$ | C． | $\sqrt{24}÷\sqrt{3}=4$ | D． | $\sqrt{（-3）^{2}}=-3$ |
尺规作图
19．
如图，AD、AC分别是⊙O的直径和弦，且∠CAD=30°，且∠CAD=30°，OB⊥AD，交AC于点B，若OB=5，则BC的长等于（ ）
如图，AD、AC分别是⊙O的直径和弦，且∠CAD=30°，且∠CAD=30°，OB⊥AD，交AC于点B，若OB=5，则BC的长等于（ ）| A． | 3 | B． | 3$\sqrt{2}$ | C． | 5 | D． | 5$\sqrt{2}$ |
9．要使二次根式$\sqrt{x-2}$有意义，x必须满足（ ）
| A． | x≤2 | B． | x≥2 | C． | x＜2 | D． | x＞2 |
16．我们给出如下定义：若一个四边形的两条对角线相等，则称这个四边形为等对角线四边形．下面四边形是等对角线四边形的是（ ）
| A． | 平行四边形 | B． | 矩形 | C． | 菱形 | D． | 梯形 |
如图，求证：∠A+∠B+∠C+∠D+∠E+∠F+∠G=180°．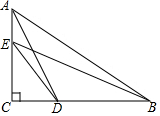
如图，在△ABC中，∠C=90°，点D，E分别在边BC，AC上，若DE=$\sqrt{5}$，AB=5，求AD2+BE2的值．