题目内容
2. 如图,在△ABC中,点P在边AB上,则在下列四个条件中::①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP•AB;④AB•CP=AP•CB,能满足△APC与△ACB相似的条件是( )
如图,在△ABC中,点P在边AB上,则在下列四个条件中::①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP•AB;④AB•CP=AP•CB,能满足△APC与△ACB相似的条件是( )| A. | ①②④ | B. | ①③④ | C. | ②③④ | D. | ①②③ |
分析 根据有两组角对应相等的两个三角形相似可对①②进行判断;根据两组对应边的比相等且夹角对应相等的两个三角形相似可对③④进行判断.
解答 解:当∠ACP=∠B,∵∠A=∠A,
所以△APC∽△ACB;
当∠APC=∠ACB,∵∠A=∠A,
所以△APC∽△ACB;
当AC2=AP•AB,
即AC:AB=AP:AC,∵∠A=∠A
所以△APC∽△ACB;
当AB•CP=AP•CB,即PC:BC=AP:AB,
而∠PAC=∠CAB,
所以不能判断△APC和△ACB相似.
故选D.
点评 本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似;有两组角对应相等的两个三角形相似.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
10.在Rt△ABC中,∠C=90°,a=3,c=5,则sinA的值是( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
17. 如图,在△ABC中,AB=AC,D为BC边上一点,且AD=AE,则∠BAD与∠EDC的关系为( )
如图,在△ABC中,AB=AC,D为BC边上一点,且AD=AE,则∠BAD与∠EDC的关系为( )
 如图,在△ABC中,AB=AC,D为BC边上一点,且AD=AE,则∠BAD与∠EDC的关系为( )
如图,在△ABC中,AB=AC,D为BC边上一点,且AD=AE,则∠BAD与∠EDC的关系为( )| A. | ∠BAD=∠EDC | B. | ∠BAD=2∠EDC | C. | ∠BAD+∠EDC=45° | D. | ∠BAD+∠EDC=60° |
11.已知$\frac{x}{y}$=$\frac{2}{3}$,则$\frac{x+y}{y}$的值为( )
| A. | $\frac{3}{2}$ | B. | $\frac{2}{5}$ | C. | $\frac{5}{3}$ | D. | $\frac{5}{2}$ |
12.下列各式结果为负数的是( )
| A. | -(-1) | B. | (-1)4 | C. | -|-1| | D. | |-2| |
 尺规作图
尺规作图 如图,求证:∠A+∠B+∠C+∠D+∠E+∠F+∠G=180°.
如图,求证:∠A+∠B+∠C+∠D+∠E+∠F+∠G=180°.
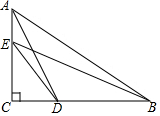 如图,在△ABC中,∠C=90°,点D,E分别在边BC,AC上,若DE=$\sqrt{5}$,AB=5,求AD2+BE2的值.
如图,在△ABC中,∠C=90°,点D,E分别在边BC,AC上,若DE=$\sqrt{5}$,AB=5,求AD2+BE2的值.