题目内容
12.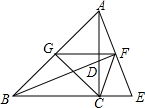 如图,△ABC为等腰直角三角形,AC=BC,点D为AC上一点,点E为BC延长线上一点,且CE=CD,连接AE交BD延长线于点F,点G为AB中点,连接CF,FG,GC,下列四个结论:①AE=BD;②△ABF≌△EBF;③∠CFE=45°;④S△AGF=S△BGC.其中正确的结论的个数为( )
如图,△ABC为等腰直角三角形,AC=BC,点D为AC上一点,点E为BC延长线上一点,且CE=CD,连接AE交BD延长线于点F,点G为AB中点,连接CF,FG,GC,下列四个结论:①AE=BD;②△ABF≌△EBF;③∠CFE=45°;④S△AGF=S△BGC.其中正确的结论的个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据SAS可以证明△BCD≌△ACE得BD=AE故①正确,由△EBF∽△EAC得$\frac{EF}{EC}=\frac{EB}{EA}$所以$\frac{EF}{EB}=\frac{EC}{EA}$推出△EFC∽△EBA得∠EFC=∠EBA=45°故③正确,点D是AC上任意一点,由∠ABF与∠EBF不一定相等,故②错误,因为∠CFE≠∠BAE,所以AB与CF不平行,所以S△BGF≠S△BGC,因为S△AGF=S△BGF所以S△AGF≠S△BGC,故④错误,.
解答 解: ∵∠ACB=90°,CA=CB,
∵∠ACB=90°,CA=CB,
∴∠CBA=∠CAB=45°,
在△BCD和△ACE中,
$\left\{\begin{array}{l}{BC=AC}\\{∠BCD=∠ACE=90°}\\{CD=CE}\end{array}\right.$,
∴△BCD≌△ACE,
∴BD=AE故①正确,
∴∠CBD=∠CAE,
∵∠CBD+∠CDB=90°,∠CDB=∠ADFM,
∴∠CAE+∠ADF=90°,
∴∠AFD=90°,
∵∠E=∠E,∠ACE=∠BFE=90°,
∴△EBF∽△EAC,
∴$\frac{EF}{EC}=\frac{EB}{EA}$,
∴$\frac{EF}{EB}=\frac{EC}{EA}$,
∵∠E=∠E,
∴△EFC∽△EBA,
∴∠EFC=∠EBA=45°故③正确,
∵点D是AC上任意一点,
∴∠ABF与∠EBF不一定相等,故②错误,
∵∠CFE≠∠BAE,
∴AB与CF不平行,
∴S△BGF≠S△BGC,
∵S△AGF=S△BGF
∴S△AGF≠S△BGC,故④错误.
故选B.
点评 本题考查全等三角形的判定和性质、相似三角形的判定和性质以及等积问题,灵活运用相似三角形是解题的关键.

练习册系列答案
相关题目
 如图,直线AB∥CD∥EF,如果∠A+∠ADF=218°,那么∠F=38°.
如图,直线AB∥CD∥EF,如果∠A+∠ADF=218°,那么∠F=38°.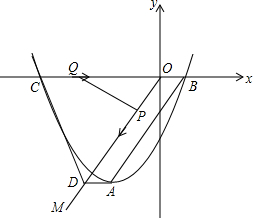 如图,顶点为A的抛物线y=a(x+2)2-4交x轴于点B(1,0),连接AB,过原点O作射线OM∥AB,过点A作AD∥x轴交OM于点D,点C为抛物线与x轴的另一个交点,连接CD.
如图,顶点为A的抛物线y=a(x+2)2-4交x轴于点B(1,0),连接AB,过原点O作射线OM∥AB,过点A作AD∥x轴交OM于点D,点C为抛物线与x轴的另一个交点,连接CD. 如图,Rt△ABC的两直角边的长为a和b,分别以它的三边为边长向外作正方形,则图中阴影三角形的面积S1,S2,S3之间的大小关系为S1=S2=S3.
如图,Rt△ABC的两直角边的长为a和b,分别以它的三边为边长向外作正方形,则图中阴影三角形的面积S1,S2,S3之间的大小关系为S1=S2=S3. 如图,∠OBC=∠OCB,∠AOB=∠AOC,证明:△ABC是等腰三角形.
如图,∠OBC=∠OCB,∠AOB=∠AOC,证明:△ABC是等腰三角形. 如图.已知OE平分∠AOB,BC⊥OA,AD⊥OB,求证:
如图.已知OE平分∠AOB,BC⊥OA,AD⊥OB,求证: