题目内容
16.一根2米长的绳子,第一次剪去一半,第二次剪去剩下的一半,如此剪下去,第六次后剩下的绳子的长度是$\frac{1}{32}$米.分析 根据题意列出算式,计算即可得到结果.
解答 解:根据题意得:第一次减去一半,剩下为2-$\frac{1}{2}$×2=2×(1-$\frac{1}{2}$)=2-1=1=($\frac{1}{2}$)0(米);
第二次减去剩下的一半,剩下为1-1×$\frac{1}{2}$=1×(1-$\frac{1}{2}$)=($\frac{1}{2}$)1(米);
第三次减去剩下的一半,剩下为$\frac{1}{2}$-$\frac{1}{2}$×$\frac{1}{2}$=$\frac{1}{2}$×(1-$\frac{1}{2}$)=$\frac{1}{4}$=($\frac{1}{2}$)2(米),
依此类推,第六次后剩下的绳子的长度是($\frac{1}{2}$)5=$\frac{1}{32}$(米),
故答案为:$\frac{1}{32}$
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
7.单项式-$\frac{1}{3}{x}^{3}{y}^{2}$的次数是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
 学校组织学生外出踏青,学生队伍从学校先步行出发,一段时间后王老师从学校骑车追赶学生,追上学生时接到电话要求王老师返回,因此王老师又立即按原速返回,当王老师回到学校时,学生还在继续前行,直到目的地.设王老师和学生队伍间的距离为y米,从王老师出发开始计时,设时间为x分钟,图中折线表示y与x的函数关系,则王老师的速度是300米/分.
学校组织学生外出踏青,学生队伍从学校先步行出发,一段时间后王老师从学校骑车追赶学生,追上学生时接到电话要求王老师返回,因此王老师又立即按原速返回,当王老师回到学校时,学生还在继续前行,直到目的地.设王老师和学生队伍间的距离为y米,从王老师出发开始计时,设时间为x分钟,图中折线表示y与x的函数关系,则王老师的速度是300米/分. 如图,在直角坐标系中,点A坐标为(0,1),点B坐标为(3,3),把线段AB平移,使得点A到达点A′(4,2),点B到达点B′,则点B′的坐标是(7,4).
如图,在直角坐标系中,点A坐标为(0,1),点B坐标为(3,3),把线段AB平移,使得点A到达点A′(4,2),点B到达点B′,则点B′的坐标是(7,4).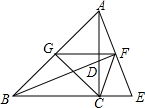 如图,△ABC为等腰直角三角形,AC=BC,点D为AC上一点,点E为BC延长线上一点,且CE=CD,连接AE交BD延长线于点F,点G为AB中点,连接CF,FG,GC,下列四个结论:①AE=BD;②△ABF≌△EBF;③∠CFE=45°;④S△AGF=S△BGC.其中正确的结论的个数为( )
如图,△ABC为等腰直角三角形,AC=BC,点D为AC上一点,点E为BC延长线上一点,且CE=CD,连接AE交BD延长线于点F,点G为AB中点,连接CF,FG,GC,下列四个结论:①AE=BD;②△ABF≌△EBF;③∠CFE=45°;④S△AGF=S△BGC.其中正确的结论的个数为( )