题目内容
1. 如图.已知OE平分∠AOB,BC⊥OA,AD⊥OB,求证:
如图.已知OE平分∠AOB,BC⊥OA,AD⊥OB,求证:(1)EC=DE;
(2)AD=BC.
分析 (1)根据角平分线的定义可得∠AOE=∠BOE,根据垂直的定义可得∠OCE=∠ODE=90°,然后利用“角角边”证明△OCE和△ODE全等,根据全等三角形对应边相等证明即可;
(2)利用(1)中的结论,结合∠OCE=∠ODE=90°,∠COB=∠DOA,证得△OCB和△ODA全等,根据全等三角形对应边相等证明即可.
解答 证明:(1)∵OE平分∠AOB,
∴∠AOE=∠BOE,
∵BC、AD分别垂直于OA、OB,
∴∠OCE=∠ODE=90°,
在△OCE和△ODE中,
$\left\{\begin{array}{l}{∠AOE=∠BOE}\\{∠OCE=∠ODE=90°}\\{OE=OE}\end{array}\right.$,
∴△OCE≌△ODE(AAS),
∴EC=DE.
(2)在△OCB和△ODA中,
$\left\{\begin{array}{l}{∠OCB=∠ODA}\\{EC=DE}\\{∠COB=DOA}\end{array}\right.$,
∴△OCB≌△ODA,
∴BC=AD.
点评 本题考查了全等三角形的判定与性质,角平分线的定义,垂直的定义,熟练掌握三角形全等的判定方法是解题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
4.计算:
(1)(-$\frac{3}{4}$)×(-1$\frac{1}{2}$)÷(-2$\frac{1}{4}$)
(2)-42-9÷(-$\frac{3}{4}$)+(-2)×(-1)2015.
(1)(-$\frac{3}{4}$)×(-1$\frac{1}{2}$)÷(-2$\frac{1}{4}$)
(2)-42-9÷(-$\frac{3}{4}$)+(-2)×(-1)2015.
11.对50个数据进行处理时,适当分组,各组数据个数之和与频率等于( )
| A. | 1,50 | B. | 1,1 | C. | 50,50 | D. | 50,1 |
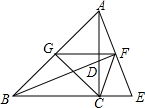 如图,△ABC为等腰直角三角形,AC=BC,点D为AC上一点,点E为BC延长线上一点,且CE=CD,连接AE交BD延长线于点F,点G为AB中点,连接CF,FG,GC,下列四个结论:①AE=BD;②△ABF≌△EBF;③∠CFE=45°;④S△AGF=S△BGC.其中正确的结论的个数为( )
如图,△ABC为等腰直角三角形,AC=BC,点D为AC上一点,点E为BC延长线上一点,且CE=CD,连接AE交BD延长线于点F,点G为AB中点,连接CF,FG,GC,下列四个结论:①AE=BD;②△ABF≌△EBF;③∠CFE=45°;④S△AGF=S△BGC.其中正确的结论的个数为( )
 如图,已知AB=AD,∠BAC=∠DAC,求证:BC=CD.
如图,已知AB=AD,∠BAC=∠DAC,求证:BC=CD.