题目内容
7.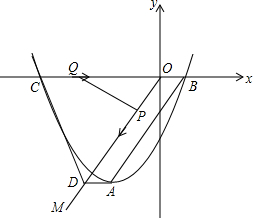 如图,顶点为A的抛物线y=a(x+2)2-4交x轴于点B(1,0),连接AB,过原点O作射线OM∥AB,过点A作AD∥x轴交OM于点D,点C为抛物线与x轴的另一个交点,连接CD.
如图,顶点为A的抛物线y=a(x+2)2-4交x轴于点B(1,0),连接AB,过原点O作射线OM∥AB,过点A作AD∥x轴交OM于点D,点C为抛物线与x轴的另一个交点,连接CD.(1)求抛物线的解析式、直线AB的解析式;
(2)若动点P从点O出发,以每秒1个单位长度的速度沿线段OD向点D运动,同时动点Q从点C出发,以每秒2个单位长度的速度沿线段CO向点O运动,当其中一个点停止运动时另一个点也随之停止运动.
问题一:当t为何值时,△OPQ为等腰三角形?
问题二:当t为何值时,四边形CDPQ的面积最小?并求此时PQ的长.
分析 (1)把点B坐标代入抛物线解析式即可求出a的值,写出顶点A的坐标,运用待定系数法即可求出直线AB的解析式;
(2)问题一,先用t表示OQ,OP的长度,再分类列出方程求解即可得出t的值,问题二:写出四边形面积关于t的二次函数,求最大值即可.
解答 解:(1)由顶点为A的抛物线y=a(x+2)2-4交x轴于点B(1,0)可得:
0=a(1+2)2-4,解得:a=$\frac{4}{9}$,
∴抛物线的解析式:$y=\frac{4}{9}(x+2)^{2}-4$,
顶点A(-2,-4),
设直线AB:y=bx+k,带入点A,B两点坐标得:$\left\{\begin{array}{l}{-4=-2b+k}\\{0=b+k}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=\frac{4}{3}}\\{k=-\frac{4}{3}}\end{array}\right.$,
∴直线AB的解析式:y=$\frac{4}{3}x-\frac{4}{3}$,
(2)如图:
∵OD∥AB,所以得直线OD:y=$\frac{4}{3}x$,
∵AD∥x轴,解得点D(-3,-4),
解得OD=5,tan∠COD=$\frac{4}{3}$,sin∠COD=$\frac{4}{5}$,cos∠COD=$\frac{3}{5}$,
把y=0带入抛物线解析式得:0=$\frac{4}{9}(x+2)^{2}-4$,
解得:x=1,或x=-5,
所以点C(-5,0),
∴OC=5,
由2t≤5,得t≤2.5,
OP=t,OQ=5-2t,
当OP=OQ时,有:t=5-2t,解得t=$\frac{5}{3}$,
当OQ=QP时,有:t=2(5-2t)×$\frac{3}{5}$,解得t=$\frac{30}{17}$,
当QP=OP时,有:5-2t=2t×$\frac{3}{5}$,解得t=$\frac{25}{16}$,
综上所述,当t为$\frac{5}{3}$,$\frac{30}{17}$,$\frac{25}{16}$时,△OPQ为等腰三角形;
四边形CDPQ的面积=S△QCD-S△OQP=$\frac{1}{2}$×5×4-$\frac{1}{2}$×(5-2t)×t×$\frac{4}{5}$=$\frac{4}{5}{t}^{2}-2t+10$,
所以当t=$-\frac{-2}{2×\frac{4}{5}}$=$\frac{5}{4}$时,四边形CDPQ的面积有最小值,
此时,OQ=$\frac{5}{2}$,OP=$\frac{5}{4}$,sin∠COD=$\frac{4}{5}$,cos∠COD=$\frac{3}{5}$,
可求得PQ=$\frac{\sqrt{65}}{4}$.
点评 此题主要考查二次函数的综合问题,会运用待定系数法求函数解析式,会分类等腰三角形的问题,会构造二次函数解解决面积的最值问题,会解直角三角形是解题的关键.

| A. | $\sqrt{16}$=±4 | B. | $\sqrt{{a}^{2}}$=a | C. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{6}$ | D. | ($\sqrt{3}$)2=3 |
 如图,在直角坐标系中,点A坐标为(0,1),点B坐标为(3,3),把线段AB平移,使得点A到达点A′(4,2),点B到达点B′,则点B′的坐标是(7,4).
如图,在直角坐标系中,点A坐标为(0,1),点B坐标为(3,3),把线段AB平移,使得点A到达点A′(4,2),点B到达点B′,则点B′的坐标是(7,4).
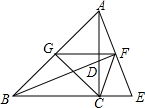 如图,△ABC为等腰直角三角形,AC=BC,点D为AC上一点,点E为BC延长线上一点,且CE=CD,连接AE交BD延长线于点F,点G为AB中点,连接CF,FG,GC,下列四个结论:①AE=BD;②△ABF≌△EBF;③∠CFE=45°;④S△AGF=S△BGC.其中正确的结论的个数为( )
如图,△ABC为等腰直角三角形,AC=BC,点D为AC上一点,点E为BC延长线上一点,且CE=CD,连接AE交BD延长线于点F,点G为AB中点,连接CF,FG,GC,下列四个结论:①AE=BD;②△ABF≌△EBF;③∠CFE=45°;④S△AGF=S△BGC.其中正确的结论的个数为( ) 如图,已知等腰三角形△ABC,底角∠B=40°,CE是∠ACB的平分线,D是底边BC上一点,满足∠CAD=20°,若EF=1,则BE=1.
如图,已知等腰三角形△ABC,底角∠B=40°,CE是∠ACB的平分线,D是底边BC上一点,满足∠CAD=20°,若EF=1,则BE=1. 如图,已知AB=AD,∠BAC=∠DAC,求证:BC=CD.
如图,已知AB=AD,∠BAC=∠DAC,求证:BC=CD.