题目内容
9.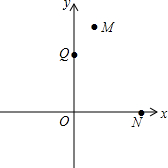 已知,在平面直角坐标系中,点M、N的坐标分别为(1,4)和(3,0),点Q是y轴上的一个动点,且M、N、Q三点不在同一直线上,当△MNQ的周长最小时,求点Q的坐标.
已知,在平面直角坐标系中,点M、N的坐标分别为(1,4)和(3,0),点Q是y轴上的一个动点,且M、N、Q三点不在同一直线上,当△MNQ的周长最小时,求点Q的坐标.
分析 根据平面直角坐标系找出N关于y轴的对称点N′位置,连接MN′,根据轴对称确定最短路线问题交点即为△MNQ的周长最小的点Q的位置,根据MD和N′D确定△MDN′是等腰直角三角形,进而求得△QON′是等腰直角三角形,即可求得OQ的长.
解答 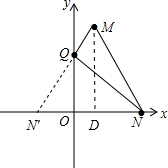 解:作点N关于y轴的对称点N′,连接MN′交y轴于点Q,
解:作点N关于y轴的对称点N′,连接MN′交y轴于点Q,
则此时△MNQ的周长最小,
理由:∵点N的坐标是(3,0),
∴点N′的坐标是(-3,0),
过点M作MD⊥x轴,垂足为点D
∵点M的坐标是(1,4)
∴N′D=MD=4
∴∠MN′D=45°,
∴N′O=OQ=3,
即点Q的坐标是(0,3).
点评 本题考查了利用轴对称变换作图,坐标与图形性质,轴对称确定最短路线问题,根据已知得出C点位置是解题关键.

练习册系列答案
相关题目
20.如图所示的网格中各有不同的图案,不能通过平移得到的是( )
| A. |  | B. |  | C. |  | D. |  |
17.下列调查中,适合采用全面调查方式的是( )
| A. | 对剡溪水质情况的调查 | |
| B. | 对端午节期间市场上粽子质量情况的调查 | |
| C. | 对某班50名同学体重情况的调查 | |
| D. | 对某品牌日光灯质量情况的调查 |

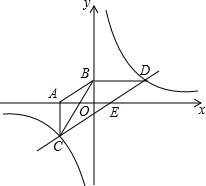 在直角坐标系中,已知反比例函数y=$\frac{k}{x}$(k≠0)图象经过点D(5,1),且BD⊥y轴,垂足为B,点C是第三象限图象上的动点,过C作CA⊥x轴,垂足为A,连接AB,BC.
在直角坐标系中,已知反比例函数y=$\frac{k}{x}$(k≠0)图象经过点D(5,1),且BD⊥y轴,垂足为B,点C是第三象限图象上的动点,过C作CA⊥x轴,垂足为A,连接AB,BC.