题目内容
18.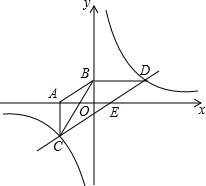 在直角坐标系中,已知反比例函数y=$\frac{k}{x}$(k≠0)图象经过点D(5,1),且BD⊥y轴,垂足为B,点C是第三象限图象上的动点,过C作CA⊥x轴,垂足为A,连接AB,BC.
在直角坐标系中,已知反比例函数y=$\frac{k}{x}$(k≠0)图象经过点D(5,1),且BD⊥y轴,垂足为B,点C是第三象限图象上的动点,过C作CA⊥x轴,垂足为A,连接AB,BC.(1)求k的值;
(2)若△BCD的面积是10,求直线CD的解析式;
(3)判断AB与CD的位置关系,并说明理由.
分析 (1)把点D的坐标代入双曲线解析式,进行计算即可得解;
(2)先根据点D的坐标求出BD的长度,再根据三角形的面积公式求出点C到BD的距离,然后求出点C的纵坐标,再代入反比例函数解析式求出点C的坐标,然后利用待定系数法求一次函数解析式解答;
(3)根据题意求出点A、B的坐标,然后利用待定系数法求出直线AB的解析式,可知与直线CD的解析式k值相等,所以AB、CD平行.
解答 解:(1)∵比例函数y=$\frac{k}{x}$(k≠0)图象经过点D(5,1),
∴k=5×1=5;
(2)设点C到BD的距离为h,
∵点D的坐标为(5,1),DB⊥y轴,
∴BD=5,
∴S△BCD=$\frac{1}{2}$×5•h=10,
解得h=4,
∵点C是双曲线第三象限上的动点,点D的纵坐标为1,
∴点C的纵坐标为1-4=-3,
∴$\frac{5}{x}$=-3,
解得x=-$\frac{5}{3}$,
∴点C的坐标为(-$\frac{5}{3}$,-3),
设直线CD的解析式为y=kx+b,
则$\left\{\begin{array}{l}{-\frac{5}{3}k+b=-3}\\{5k+b=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{3}{5}}\\{b=-2}\end{array}\right.$,
所以,直线CD的解析式为y=$\frac{3}{5}$x-2;
(3)AB∥CD.
理由如下:∵CA⊥x轴,DB⊥y轴,设点C的坐标为(c,$\frac{5}{c}$),点D的坐标为(5,1),
∴点A、B的坐标分别为A(c,0),B(0,1),
设直线AB的解析式为y=mx+n,
则$\left\{\begin{array}{l}{mc+n=0}\\{n=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=-\frac{1}{c}}\\{n=1}\end{array}\right.$,
所以,直线AB的解析式为y=-$\frac{1}{c}$x+1,
设直线CD的解析式为y=ex+f,
则$\left\{\begin{array}{l}{ec+f=\frac{5}{c}}\\{5e+f=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{e=-\frac{1}{c}}\\{f=\frac{c+5}{c}}\end{array}\right.$,
∴直线CD的解析式为y=-$\frac{1}{c}$x+$\frac{c+5}{c}$,
∵AB、CD的解析式k都等于-$\frac{1}{c}$,
∴AB与CD的位置关系是AB∥CD.
点评 本题是对反比例函数的综合考查,主要利用了待定系数法求函数解析式,三角形的面积的求解,待定系数法是求函数解析式最常用的方法,一定要熟练掌握并灵活运用.

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案| A. | a>b | B. | b>a | C. | a≥b | D. | b≥a |
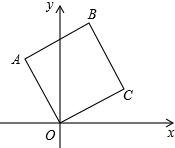 如图,在平面直角坐标系中,四边形ABCO是正方形,已知点C的坐标为($\sqrt{3}$,1),则点B的坐标为( )
如图,在平面直角坐标系中,四边形ABCO是正方形,已知点C的坐标为($\sqrt{3}$,1),则点B的坐标为( )| A. | ($\sqrt{3}$-1,$\sqrt{3}$+1) | B. | ($\sqrt{3}$-1,1) | C. | (1,$\sqrt{3}$+1) | D. | ($\sqrt{3}$-1,2) |
| A. | 了解全校同学喜欢课程情况,对某班男生进行调查 | |
| B. | 了解某小区居民的防火意识,从每幢居民随机抽若干人进行调查 | |
| C. | 了解商场的平均日营业额,选在周末进行调查 | |
| D. | 了解杭州城区空气质量,在江干区设点调查 |
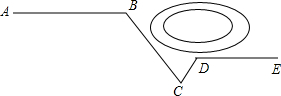 如图,煤气公司安装煤气管道,他们从点A处铺设到点B处时,由于有一个人工湖挡住了去路,需要改变方向经过点C,再拐到点D,然后沿与AB平行的DE方向继续铺设.如图∠BCD=50°,∠ABC=120°,求∠CDE的大小.
如图,煤气公司安装煤气管道,他们从点A处铺设到点B处时,由于有一个人工湖挡住了去路,需要改变方向经过点C,再拐到点D,然后沿与AB平行的DE方向继续铺设.如图∠BCD=50°,∠ABC=120°,求∠CDE的大小.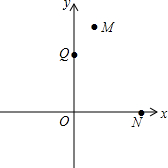 已知,在平面直角坐标系中,点M、N的坐标分别为(1,4)和(3,0),点Q是y轴上的一个动点,且M、N、Q三点不在同一直线上,当△MNQ的周长最小时,求点Q的坐标.
已知,在平面直角坐标系中,点M、N的坐标分别为(1,4)和(3,0),点Q是y轴上的一个动点,且M、N、Q三点不在同一直线上,当△MNQ的周长最小时,求点Q的坐标.