题目内容
14.在Rt△ACB和Rt△AEF中,∠ACB=∠AEF=90°,若点P是BF的中点,连接PC,PE.特殊发现:
如图1,若点E,F分别落在边AB,AC上,则结论:PC=PE成立(不要求证明).
问题探究:
把图1中的△AEF绕着点A顺时针旋转.
(1)如图2,若点E落在边CA的延长线上,则上述结论是否成立?若成立,请给予证明;若不成立,请说明理由;
(2)如图3,若点F落在边AB上,则上述结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由;
(3)记$\frac{AC}{BC}$=k,当k为何值时,△CPE总是等边三角形?(请直接写出k的值,不必说明理由)

分析 (1)首先过点P作PM⊥CE于点M,然后根据EF⊥AE,BC⊥AC,可得EF∥MP∥CB,推得$\frac{EM}{MC}=\frac{FP}{PB}$,再根据点P是BF的中点,可得EM=MC,据此推得PC=PE即可.
(2)首先过点F作FD⊥AC于点D,过点P作PM⊥AC于点M,连接PD,然后根据全等三角形判定的方法,判断出△DAF≌△EAF,即可判断出AD=AE;再判断出△DAP≌△EAP,即可判断出PD=PE;最后根据FD⊥AC,BC⊥AC,PM⊥AC,可得FD∥BC∥PM,再根据点P是BF的中点,推得PC=PD,再根据PD=PE,即可推得PC=PE.
(3)首先根据△CPE总是等边三角形,可得将△AEF绕着点A顺时针旋转180°,△CPE仍是等边三角形;然后根据∠BCF=∠BEF=90°,点P是BF的中点,可得点C、E在以点P为圆心,BF为直径的圆上;最后根据圆周角定理,求出∠CBE的度数,即可求出当△CPE总是等边三角形时,k的值是多少.
解答 解:(1)如图2,过点P作PM⊥CE于点M,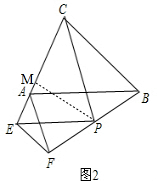 ,
,
PC=PE成立,理由如下:
∵EF⊥AE,BC⊥AC,
∴EF∥MP∥CB,
∴$\frac{EM}{MC}=\frac{FP}{PB}$,
∵点P是BF的中点,
∴EM=MC,
又∵PM⊥CE,
∴PC=PE.
(2)如图3,过点F作FD⊥AC于点D,过点P作PM⊥AC于点M,连接PD,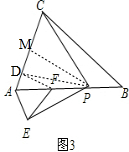 ,
,
PC=PE成立,理由如下:
∵∠DAF=∠EAF,∠FDA=∠FEA=90°,
在△DAF和△EAF中,
$\left\{\begin{array}{l}{∠DAF=∠EAF}\\{∠FDA=∠FEA}\\{AF=AF}\end{array}\right.$,
∴△DAF≌△EAF(AAS),
∴AD=AE,
在△DAP和△EAP中,
$\left\{\begin{array}{l}{AD=AE}\\{∠DAP=∠EAP}\\{AP=AP}\end{array}\right.$,
∴△DAP≌△EAP(SAS),
∴PD=PE,
∵FD⊥AC,BC⊥AC,PM⊥AC,
∴FD∥BC∥PM,
∴$\frac{DM}{MC}=\frac{FP}{PB}$,
∵点P是BF的中点,
∴DM=MC,
又∵PM⊥AC,
∴PC=PD,
又∵PD=PE,
∴PC=PE.
(3)如图4,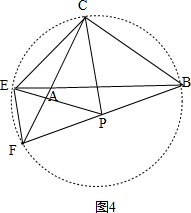 ,
,
∵△CPE总是等边三角形,
∴将△AEF绕着点A顺时针旋转180°,△CPE仍是等边三角形,
∵∠BCF=∠BEF=90°,点P是BF的中点,
∴点C、E在以点P为圆心,BF为直径的圆上,
∵△CPE是等边三角形,
∴∠CPE=60°,
根据圆周角定理,可得
∠CBE=$\frac{1}{2}$∠CPE=$\frac{1}{2}×$60°=30°,
即∠ABC=30°,
在Rt△ABC中,
∵$\frac{AC}{BC}$=k,$\frac{AC}{BC}$=tan30°,
∴k=tan30°=$\frac{\sqrt{3}}{3}$,
∴当k为$\frac{\sqrt{3}}{3}$时,△CPE总是等边三角形.
点评 (1)此题主要考查了几何变换综合题,考查了分析推理能力,考查了数形结合思想的应用,要熟练掌握.
(2)此题还考查了全等三角形判定和性质的应用,以及直角三角形的性质和应用,要熟练掌握.
(3)解答第(3)题时,理解“△CPE总是等边三角形”的含义是解答此题的关键所在.

| 甲种货车 | 乙种货车 | |
| 载货量(吨/辆) | 45 | 30 |
| 租金(元/辆) | 400 | 300 |
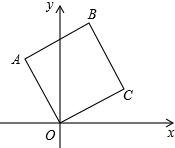 如图,在平面直角坐标系中,四边形ABCO是正方形,已知点C的坐标为($\sqrt{3}$,1),则点B的坐标为( )
如图,在平面直角坐标系中,四边形ABCO是正方形,已知点C的坐标为($\sqrt{3}$,1),则点B的坐标为( )| A. | ($\sqrt{3}$-1,$\sqrt{3}$+1) | B. | ($\sqrt{3}$-1,1) | C. | (1,$\sqrt{3}$+1) | D. | ($\sqrt{3}$-1,2) |
| 第一套 | 第二套 | |
| 椅子高度x(cm) | 42 | 38 |
| 课桌高度y(cm) | 74 | 70 |
(2)现有一张高80cm的课桌和一张高为43cm的椅子,它们是否配套?为什么?
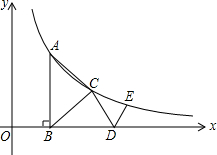 如图,△ABC是等腰直角三角形,斜边AB⊥x轴于B,顶点A,C在反比例函数y=$\frac{2}{x}$(x>0)的图象上,再作等腰Rt△CDE,使直角顶点E在该函数图象上,顶点D在x轴正半轴上,则△CDE的面积是$\frac{11-6\sqrt{3}}{2}$.
如图,△ABC是等腰直角三角形,斜边AB⊥x轴于B,顶点A,C在反比例函数y=$\frac{2}{x}$(x>0)的图象上,再作等腰Rt△CDE,使直角顶点E在该函数图象上,顶点D在x轴正半轴上,则△CDE的面积是$\frac{11-6\sqrt{3}}{2}$.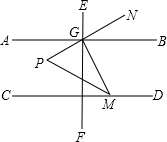 已知,如图,直线AB∥CD,直线EF⊥AB,点M在CD上,MP平分∠GMC,PN平分∠EGM,且∠CMG+∠MGF=90°.
已知,如图,直线AB∥CD,直线EF⊥AB,点M在CD上,MP平分∠GMC,PN平分∠EGM,且∠CMG+∠MGF=90°.
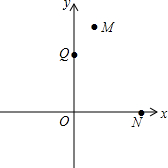 已知,在平面直角坐标系中,点M、N的坐标分别为(1,4)和(3,0),点Q是y轴上的一个动点,且M、N、Q三点不在同一直线上,当△MNQ的周长最小时,求点Q的坐标.
已知,在平面直角坐标系中,点M、N的坐标分别为(1,4)和(3,0),点Q是y轴上的一个动点,且M、N、Q三点不在同一直线上,当△MNQ的周长最小时,求点Q的坐标.