题目内容
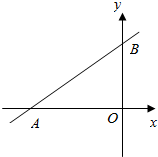 如图,直线l与x、y轴分别交于点M(-4,0),N(0,3),现将直线l向右平移,速度为2个单位/s,与x、y轴交点为A、B,点P从点M出发,向右运动,速度为1个单位/s,设运动时间为t.
如图,直线l与x、y轴分别交于点M(-4,0),N(0,3),现将直线l向右平移,速度为2个单位/s,与x、y轴交点为A、B,点P从点M出发,向右运动,速度为1个单位/s,设运动时间为t.(1)求点A、B的坐标;
(2)当以O为圆心,t为半径的圆与直线l相切时,求t的值.
考点:圆的综合题
专题:
分析:(1)由条件可知OM=4,ON=3,则OA=4-2t,再利用△OMN∽△OAB,可求出OB,可求得A、B点的坐标;
(2)当直线和圆相切时,利用点O到直线l的距离等于t,结合三角形相似得到对应线段成比例,得到关于t的方程,求解即可.
(2)当直线和圆相切时,利用点O到直线l的距离等于t,结合三角形相似得到对应线段成比例,得到关于t的方程,求解即可.
解答:解:(1)由平移可知AB∥MN,
∴△OMN∽△OAB,
∴
=
,
∵M(-4,0),N(0,3),
∴OM=4,ON=3,
∵直线l向右平移,速度为2个单位/s,
∴MA=2t,
当0≤t≤2,即A在线段OM上时,如图1,OA=4-2t,此时
=
,解得OB=3-
t,

因为A点在x轴负半轴,B点在y轴正半轴上,
所以点A坐标为(2t-4,0),B点坐标为(0,3-
t);
当t>2,即A在x轴正半轴上时,如图2,OA=2t-4,此时
=
,解得OB=
t-3,

因为A点在x正半轴,B点在y负半轴上,
所以A点坐标为(2t-4,0),B点坐标为(0,3-
t);
综上可知A点坐标为(2t-4,0)或(4+2t,0),B点坐标为(0,3-
t);
(2)当0≤t≤2,即A在线段OM上时,如图3,设AB和⊙O相切于点Q,连接OQ,则OQ=t,且OQ⊥AB,

∵AB∥MN,
∴∠BAO=∠NMO,且∠OQA=∠MON,
∴△AOQ~△MNO,
∴
=
,
∵OM=4,ON=3,
∴MN=5,此时OA=4-2t,
∴
=
,解得t=
;
当t>2,即A在x轴正半轴上时,如图4,设AB和⊙O相切于点Q,连接OQ,则OQ=t,且OQ⊥AB,

同理可得△AOQ~△MNO,
∴
=
,
∵OM=4,ON=3,
∴MN=5,此时OA=2t-4,
∴
=
,解得t=12.
综上可知当t=
s或12s时以O为圆心,t为半径的圆与直线l相切.
∴△OMN∽△OAB,
∴
| OA |
| OM |
| OB |
| ON |
∵M(-4,0),N(0,3),
∴OM=4,ON=3,
∵直线l向右平移,速度为2个单位/s,
∴MA=2t,
当0≤t≤2,即A在线段OM上时,如图1,OA=4-2t,此时
| 4-2t |
| 4 |
| OB |
| 3 |
| 3 |
| 2 |

因为A点在x轴负半轴,B点在y轴正半轴上,
所以点A坐标为(2t-4,0),B点坐标为(0,3-
| 3 |
| 2 |
当t>2,即A在x轴正半轴上时,如图2,OA=2t-4,此时
| 2t-4 |
| 4 |
| OB |
| 3 |
| 3 |
| 2 |

因为A点在x正半轴,B点在y负半轴上,
所以A点坐标为(2t-4,0),B点坐标为(0,3-
| 3 |
| 2 |
综上可知A点坐标为(2t-4,0)或(4+2t,0),B点坐标为(0,3-
| 3 |
| 2 |
(2)当0≤t≤2,即A在线段OM上时,如图3,设AB和⊙O相切于点Q,连接OQ,则OQ=t,且OQ⊥AB,

∵AB∥MN,
∴∠BAO=∠NMO,且∠OQA=∠MON,
∴△AOQ~△MNO,
∴
| OQ |
| ON |
| OA |
| MN |
∵OM=4,ON=3,
∴MN=5,此时OA=4-2t,
∴
| t |
| 3 |
| 4-2t |
| 5 |
| 12 |
| 11 |
当t>2,即A在x轴正半轴上时,如图4,设AB和⊙O相切于点Q,连接OQ,则OQ=t,且OQ⊥AB,

同理可得△AOQ~△MNO,
∴
| OQ |
| ON |
| OA |
| MN |
∵OM=4,ON=3,
∴MN=5,此时OA=2t-4,
∴
| t |
| 3 |
| 2t-4 |
| 5 |
综上可知当t=
| 12 |
| 11 |
点评:本题主要考查切线的性质及相似三角形的判定和性质的综合应用,在解题中分A点在x正半轴和x负半轴两种情况是解题的关键.

练习册系列答案
相关题目
 如图,已知四边形ABCD为正方形,OB=OC,∠BOC=150°,求证:△AOD为等边三角形.
如图,已知四边形ABCD为正方形,OB=OC,∠BOC=150°,求证:△AOD为等边三角形.