题目内容
(1)当a=1,b=1时,比较a2+b2与2ab的大小;
(2)当a=-2,b=3时,比较a2+b2与2ab的大小;
(3)再任取a,b的任意一组的值,通过计算比较a2+b2与2ab的大小,你能得到什么结论?并说明理由.
(2)当a=-2,b=3时,比较a2+b2与2ab的大小;
(3)再任取a,b的任意一组的值,通过计算比较a2+b2与2ab的大小,你能得到什么结论?并说明理由.
考点:代数式求值
专题:计算题
分析:(1)把a与b代入两式计算,比较即可得到结果;
(2)把a与b代入两式计算,比较即可得到结果;
(3)把a=3,b=-2代入两式计算,比较大小,得到一般性结论即可.
(2)把a与b代入两式计算,比较即可得到结果;
(3)把a=3,b=-2代入两式计算,比较大小,得到一般性结论即可.
解答:解:(1)当a=1,b=1时,a2+b2=1+1=2,2ab=2,即a2+b2=2ab;
(2)当a=-2,b=3时,a2+b2=4+9=13,2ab=-12,即a2+b2>2ab;
(3)当a=3,b=-2时,a2+b2=9+4=13,2ab=-12,即a2+b2>2ab,
结论为a2+b2≥2ab,理由为:
∵(a-b)2=a2+b2-2ab≥0,
∴a2+b2≥2ab.
(2)当a=-2,b=3时,a2+b2=4+9=13,2ab=-12,即a2+b2>2ab;
(3)当a=3,b=-2时,a2+b2=9+4=13,2ab=-12,即a2+b2>2ab,
结论为a2+b2≥2ab,理由为:
∵(a-b)2=a2+b2-2ab≥0,
∴a2+b2≥2ab.
点评:此题考查了代数式求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
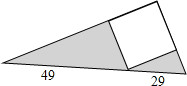 如图所示,空白部分是正方形,求阴影部分的面积.
如图所示,空白部分是正方形,求阴影部分的面积.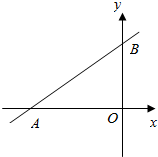 如图,直线l与x、y轴分别交于点M(-4,0),N(0,3),现将直线l向右平移,速度为2个单位/s,与x、y轴交点为A、B,点P从点M出发,向右运动,速度为1个单位/s,设运动时间为t.
如图,直线l与x、y轴分别交于点M(-4,0),N(0,3),现将直线l向右平移,速度为2个单位/s,与x、y轴交点为A、B,点P从点M出发,向右运动,速度为1个单位/s,设运动时间为t.