题目内容
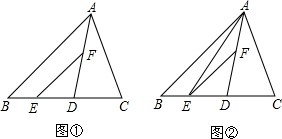
 如图,已知四边形ABCD为正方形,OB=OC,∠BOC=150°,求证:△AOD为等边三角形.
如图,已知四边形ABCD为正方形,OB=OC,∠BOC=150°,求证:△AOD为等边三角形.考点:正方形的性质,等边三角形的判定
专题:证明题
分析:根据正方形的轴对称性判断出OA=OD,设正方形的边长为a,根据等边对等角求出∠OBC=15°,然后利用15°角的正切值求出点O到BC的距离,再求出点O到AD的距离,然后利用锐角三角函数求出∠OAD=60°,再根据有一个角是60°的等腰三角形是等边三角形证明.
解答:证明:∵四边形ABCD为正方形,OB=OC,
∴OA=OD,
∵OB=OC,∠BOC=150°,
∴∠OBC=
(180°-150°)=15°,
设正方形的边长为a,
则点O到BC的距离=
BC•tan15°=
a(2-
),
所以点O到AD的距离=a-
a(2-
)=
a,
所以tan∠OAD=
=
,
所以∠OAD=60°,
又∵OA=OD,
∴△AOD为等边三角形.
∴OA=OD,
∵OB=OC,∠BOC=150°,
∴∠OBC=
| 1 |
| 2 |
设正方形的边长为a,
则点O到BC的距离=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
所以点O到AD的距离=a-
| 1 |
| 2 |
| 3 |
| ||
| 2 |
所以tan∠OAD=
| ||||
|
| 3 |
所以∠OAD=60°,
又∵OA=OD,
∴△AOD为等边三角形.
点评:本题考查了正方形的性质,等边三角形的判定,等边对等角的性质,锐角三角函数的定义,考虑利用三角函数求解更简便,关键在于判断出∠OAD=60°.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
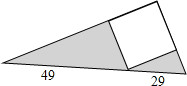 如图所示,空白部分是正方形,求阴影部分的面积.
如图所示,空白部分是正方形,求阴影部分的面积.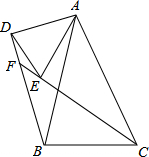 如图,AB=AC,AD=AE,∠DAE=∠BAC=α,CE的延长线交BD于F.
如图,AB=AC,AD=AE,∠DAE=∠BAC=α,CE的延长线交BD于F. 已知:如图,在平面直角坐标系中,Rt△OCD的一边OC在x轴上,∠C=90°,点D在第一象限,OC=3,DC=4,反比例函数的图象经过OD的中点A.
已知:如图,在平面直角坐标系中,Rt△OCD的一边OC在x轴上,∠C=90°,点D在第一象限,OC=3,DC=4,反比例函数的图象经过OD的中点A.
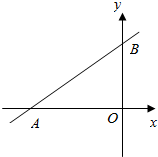 如图,直线l与x、y轴分别交于点M(-4,0),N(0,3),现将直线l向右平移,速度为2个单位/s,与x、y轴交点为A、B,点P从点M出发,向右运动,速度为1个单位/s,设运动时间为t.
如图,直线l与x、y轴分别交于点M(-4,0),N(0,3),现将直线l向右平移,速度为2个单位/s,与x、y轴交点为A、B,点P从点M出发,向右运动,速度为1个单位/s,设运动时间为t.