题目内容
在△ABC中,∠A=90°,BD为角平分线,DE⊥BC于E,且E恰为BC中点,则∠ABC等于 .
考点:线段垂直平分线的性质
专题:
分析:由DE⊥BC,且E恰为BC中点,可得BD=CD,又由在△ABC中,∠A=90°,BD为角平分线,即可求得∠ABD=∠DBC=∠C,继而求得答案.
解答: 解:∵DE⊥BC,且E恰为BC中点,
解:∵DE⊥BC,且E恰为BC中点,
∴BD=CD,
∴∠DBC=∠C,
∵BD为角平分线,
∴∠ABD=∠DBC,
∴∠ABD=∠DBC=∠C,
∵在△ABC中,∠A=90°,
∴∠C=30°,
∴∠ABC=60°.
故答案为:60°.
 解:∵DE⊥BC,且E恰为BC中点,
解:∵DE⊥BC,且E恰为BC中点,∴BD=CD,
∴∠DBC=∠C,
∵BD为角平分线,
∴∠ABD=∠DBC,
∴∠ABD=∠DBC=∠C,
∵在△ABC中,∠A=90°,
∴∠C=30°,
∴∠ABC=60°.
故答案为:60°.
点评:此题考查了线段垂直平分线的性质以及等腰三角形的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
如果一个三角形的三个外角之比为2:3:4,则与之对应的三个内角度数之比为( )
| A、4:3:2 | B、5:3:1 |
| C、3:2:4 |
方程(x-3)2=m2的解是( )
| A、x1=m,x2=-m |
| B、x1=3+m,x2=3-m |
| C、x1=3+m,x2=-3-m |
| D、x1=3+m,x2=-3+m |
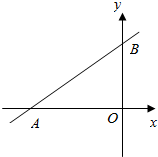 如图,直线l与x、y轴分别交于点M(-4,0),N(0,3),现将直线l向右平移,速度为2个单位/s,与x、y轴交点为A、B,点P从点M出发,向右运动,速度为1个单位/s,设运动时间为t.
如图,直线l与x、y轴分别交于点M(-4,0),N(0,3),现将直线l向右平移,速度为2个单位/s,与x、y轴交点为A、B,点P从点M出发,向右运动,速度为1个单位/s,设运动时间为t.