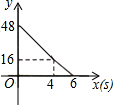题目内容
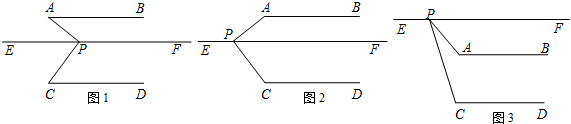
12.已知线段AB∥CD,直线EF∥AB,若点P在直线EF上,连接PA、PC.(1)如图1,直线EF在线段AB、CD之间,点P在中间位置时,写出∠A、∠C、∠APC三个角之间的数量关系,并证明你的结论;
(2)如图2,直线EF在线段AB、CD之间,点P在偏左位置时,写出∠A、∠C、∠APC三个角之间的数量关系,并证明你的结论;
(3)如图3,直线EF在线段AB上方,点P在偏左位置时,写出∠PAB、∠PCD、∠APC三个角之间的数量关系,并证明你的结论.
分析 (1)∠APC=∠A+∠C,利用两直线平行,内错角相等来证明;
(2)∠APC+∠A+∠C=360°,利用两直线平行,同旁内角互补来证明;
(3)∠PAB=∠PCD+∠APC,利用两直线平行,同旁内角互补来证明.
解答 解:(1)∠APC=∠A+∠C.
证明:∵线段AB∥CD,直线EF∥AB,
∴∠A=∠APE,∠C=∠CPE,
∵∠APC=∠APE+∠CPE,
∴∠APC=∠A+∠C.
(2)∠APC+∠A+∠C=360°.
证明:∵线段AB∥CD,直线EF∥AB,
∴∠A+∠APF=180°,∠C+∠CPF=180°,
∴∠A+∠APF+∠C+∠CPF=∠A+∠C+∠APC=360°
(3)∠PAB=∠PCD+∠APC.
证明:∵线段AB∥CD,直线EF∥AB,
∴∠APF+∠PAB=180°,∠CPF+∠PCD=180°,
∵∠APC=∠CPF-∠APF,
∴∠CPF+∠PCD-(∠APF+∠PAB)=(∠CPF-∠APF)+∠PCD-∠PAB=0°,
∴∠PAB=∠PCD+∠APC.
点评 本题考查了平行线的性质,解题的关键是:(1)两直线平行,内错角相等;(2)两直线平行,同旁内角互补;(3)两直线平行,同旁内角互补.本题属于基础题,难度不大,根据平行线的性质结合角之间的关系即可得以解决.

练习册系列答案
相关题目
3.为确保信息安全,信息需加密传输,发送方由明文→密文(加密);接收方由密文→明文(解密).已知加密规则为:明文a,b,c,d对应密文a+2b,2b+c,2c+3d,4d.例如:明文1,2,3,4对应的密文5,7,18,16.当接收方收到密文14,9,23,28时,则解密得到的明文为( )
| A. | 4,6,1,7 | B. | 4,1,6,7 | C. | 6,4,1,7 | D. | 1,6,4,7 |
17. 如图,Rt△ABC中,∠C=90°,AC=6,BC=8,AD平分∠BAC,则点B到AD的距离是( )
如图,Rt△ABC中,∠C=90°,AC=6,BC=8,AD平分∠BAC,则点B到AD的距离是( )
 如图,Rt△ABC中,∠C=90°,AC=6,BC=8,AD平分∠BAC,则点B到AD的距离是( )
如图,Rt△ABC中,∠C=90°,AC=6,BC=8,AD平分∠BAC,则点B到AD的距离是( )| A. | 3 | B. | 4 | C. | 2$\sqrt{5}$ | D. | $\frac{{12\sqrt{13}}}{13}$ |
1.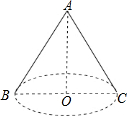 如图,圆锥的轴截面(过圆锥顶点和底面圆心的截面)△ABC是直角三角形,则圆锥的侧面展开图扇形的圆心角度约为( )
如图,圆锥的轴截面(过圆锥顶点和底面圆心的截面)△ABC是直角三角形,则圆锥的侧面展开图扇形的圆心角度约为( )
 如图,圆锥的轴截面(过圆锥顶点和底面圆心的截面)△ABC是直角三角形,则圆锥的侧面展开图扇形的圆心角度约为( )
如图,圆锥的轴截面(过圆锥顶点和底面圆心的截面)△ABC是直角三角形,则圆锥的侧面展开图扇形的圆心角度约为( )| A. | 127° | B. | 180° | C. | 201° | D. | 255° |
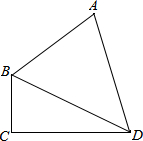 如图,四边形ABCD中,已知AB=10,CD=12,对角线BD平分∠ABC,∠ADB=45°,∠BCD=90°,则边BC的长度为4或6.
如图,四边形ABCD中,已知AB=10,CD=12,对角线BD平分∠ABC,∠ADB=45°,∠BCD=90°,则边BC的长度为4或6.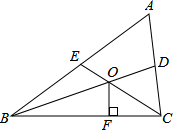 如图,△ABC 的中线BD、CE相交于点O,OF⊥BC,且AB=6,BC=5,AC=4,OF=3,则四边形ADOE的面积是7.5.
如图,△ABC 的中线BD、CE相交于点O,OF⊥BC,且AB=6,BC=5,AC=4,OF=3,则四边形ADOE的面积是7.5.
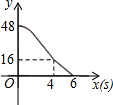
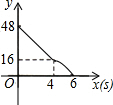
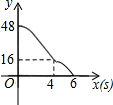
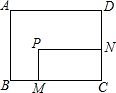 如图,矩形ABCD,AB=6,AD=8;动点M、N从点C出发,分别沿CB、CD以每秒2个单位长度和每秒1个单位长度的速度运动,分别至点B、点D停止.作矩形PMCN.若运动时间为x(单位:s),设矩形ABCD除去矩形PMCN后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是( )
如图,矩形ABCD,AB=6,AD=8;动点M、N从点C出发,分别沿CB、CD以每秒2个单位长度和每秒1个单位长度的速度运动,分别至点B、点D停止.作矩形PMCN.若运动时间为x(单位:s),设矩形ABCD除去矩形PMCN后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是( )