题目内容
8. 如图,在矩形ABCD中,AB=8,BC=4,若点M、N分别是线段AC、AB上的两个动点,则BM+MN的最小值为( )
如图,在矩形ABCD中,AB=8,BC=4,若点M、N分别是线段AC、AB上的两个动点,则BM+MN的最小值为( )| A. | 6.4 | B. | 8 | C. | 4$\sqrt{3}$ | D. | 6 |
分析 过B点作AC的垂线,使AC两边的线段相等,到E点,过E作EF垂直AB交AB于F点,EF就是所求的线段.
解答 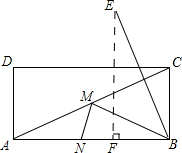 解:过B点作AC的垂线,使AC两边的线段相等,到E点,过E作EF垂直AB交AB于F点,
解:过B点作AC的垂线,使AC两边的线段相等,到E点,过E作EF垂直AB交AB于F点,
∵AB=8,BC=4,
∴AC=$\sqrt{{8}^{2}+{4}^{2}}=4\sqrt{5}$,
∴AC边上的高为$\frac{8×4}{4\sqrt{5}}=\frac{8\sqrt{5}}{5}$,所以BE=$\frac{16\sqrt{5}}{5}$.
∵△ABC∽△EFB,
∴$\frac{AB}{EF}$=$\frac{AC}{BE}$,即$\frac{8}{EF}=\frac{4\sqrt{5}}{\frac{16\sqrt{5}}{5}}$,
EF=6.4.
故选A.
点评 本题考查最短路径问题,关键确定何时路径最短,然后运用勾股定理和相似三角形的性质求得解.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
18.有40个数据,共分成6组,第1-4组的频数分别是10、5、7、6.第5组的占10%,则第6组占( )
| A. | 25% | B. | 30% | C. | 15% | D. | 20% |

 如图,△ABC绕点C旋转后,顶点A旋转到了点D.
如图,△ABC绕点C旋转后,顶点A旋转到了点D.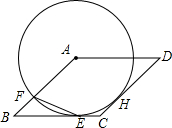 如图,⊙A与菱形ABCD的边BC相切于点E,与边AB相交于点F,连结EF
如图,⊙A与菱形ABCD的边BC相切于点E,与边AB相交于点F,连结EF