题目内容
9.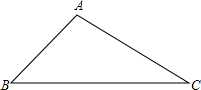 如图,在△ABC中,∠B=45°,∠C=30°,AC=2,点D在BC上,将△ACD沿直线AD翻折后,点C落在点E处,边AE交边BC于点F,如果DE∥AB,那么$\frac{CF}{BF}$的值是$\sqrt{3}$+1.
如图,在△ABC中,∠B=45°,∠C=30°,AC=2,点D在BC上,将△ACD沿直线AD翻折后,点C落在点E处,边AE交边BC于点F,如果DE∥AB,那么$\frac{CF}{BF}$的值是$\sqrt{3}$+1.
分析 作AM⊥BC垂足为M,先求出AM、BM、MC,再证明CA=CF,由此即可解决问题.
解答 解:如图作AM⊥BC垂足为M,
∵△ADE是由△ADC翻折,
∴∠C=∠E=30°,
∵AB∥DE,
∴∠E=∠BAF=30°,
∴∠AFC=∠B+∠BAF=75°,
∴∠CAF=180°-∠AFC-∠C=75°,
∴∠CAF=∠CFA=75°,
∴CA=CF=2,
在RT△AMC中,∵∠C=30°,AC=2,
∴AM=1,MC=$\sqrt{3}$,
∵∠B=∠BAM=45°,
∴MB=AM=1,
∴BC=1+$\sqrt{3}$,BF=1+$\sqrt{3}$-2=$\sqrt{3}$-1
∴$\frac{CF}{BF}$=$\frac{2}{\sqrt{3}-1}$=$\sqrt{3}$+1.
故答案为$\sqrt{3}$+1.
点评 本题考查翻折变换、等腰三角形的判定和性质、勾股定理等知识,添加辅助线构造直角三角形是解决问题的关键,解题时要善于发现特殊三角形,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.下列运算中,正确的是( )
| A. | m2•m3=m6 | B. | (-m2)3=m6 | C. | -m2-2m2=-3m2 | D. | -3m-2=-$\frac{1}{9{m}^{2}}$ |
14.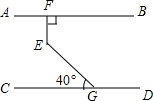 如图,AB∥CD,EF⊥AB于F,∠EGC=40°,则∠FEG=( )
如图,AB∥CD,EF⊥AB于F,∠EGC=40°,则∠FEG=( )
 如图,AB∥CD,EF⊥AB于F,∠EGC=40°,则∠FEG=( )
如图,AB∥CD,EF⊥AB于F,∠EGC=40°,则∠FEG=( )| A. | 120° | B. | 130° | C. | 140° | D. | 150° |