题目内容
17.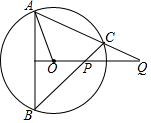 如图,AB为圆O的弦,QO⊥AB,QA交⊙O于C,BC交QO于P,求证:OA2=OP•OQ.
如图,AB为圆O的弦,QO⊥AB,QA交⊙O于C,BC交QO于P,求证:OA2=OP•OQ.
分析 欲证明OA2=OP•OQ,只要证明△AOP∽△QOA,只要证明∠OAP=∠Q即可解决问题.
解答 证明:如图连接OB、AP,延长QO交AB于H.
∵OH⊥AB,OA=OB,
∴∠AOH=∠BOH,AH=HB,
∴QH垂直平分AB,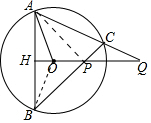
∴PA=PB,
∵∠ACB=$\frac{1}{2}$∠AOB,
∴∠ACB=∠BOH,
∴∠PCQ=∠POB,∵∠CPQ=∠OPB,
∴∠Q=∠PBO,
∵∠PAB=∠PBA,∠OAB=∠OBA,
∴∠PAO=∠PBO=∠Q,
∵∠AOP=∠AOQ,
∴△AOP∽△QOA,
∴$\frac{AO}{QO}$=$\frac{OP}{OA}$,
∴OA2=OP•OQ.
点评 本题考查垂径定理、圆周角定理、相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
7. 一个关于x的不等式的解集表示在数轴上(如图),则这个不等式可以是( )
一个关于x的不等式的解集表示在数轴上(如图),则这个不等式可以是( )
 一个关于x的不等式的解集表示在数轴上(如图),则这个不等式可以是( )
一个关于x的不等式的解集表示在数轴上(如图),则这个不等式可以是( )| A. | 2x≥-4 | B. | 2x>-4 | C. | -2x≤-4 | D. | -2x≥4 |
8.下列四个选项中,表示算式-5$\frac{3}{7}$+2计算结果,正确的是( )
| A. | $-5\frac{1}{7}$ | B. | $-3\frac{3}{7}$ | C. | $7\frac{3}{7}$ | D. | $-7\frac{3}{7}$. |
5.下列说法中不正确的是( )
| A. | -$\sqrt{5}$是5的平方根 | B. | -3是-27的立方根 | ||
| C. | 4的平方根是16 | D. | (-2)2的算术平方根是2 |
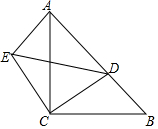 如图,等腰直角△ABC中,AC=BC,∠ACB=90°,点D为斜边AB上一点,若AB=14,BD=6,将△BCD绕点C逆时针方向旋转到△ACE的位置,对于下列说法:①△ADE是直角三角形,②△CDE是等腰三角形,③DE=10,④CD=5$\sqrt{2}$.其中正确说法是①②③④(填序号).
如图,等腰直角△ABC中,AC=BC,∠ACB=90°,点D为斜边AB上一点,若AB=14,BD=6,将△BCD绕点C逆时针方向旋转到△ACE的位置,对于下列说法:①△ADE是直角三角形,②△CDE是等腰三角形,③DE=10,④CD=5$\sqrt{2}$.其中正确说法是①②③④(填序号).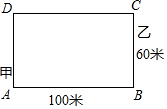 如图,有一条长方形跑道,甲从A点出发,乙从C点发.同时按逆时针方奔跑.甲速每秒6.25米,乙速每秒5米.跑道长100米,宽60米.当甲、乙每次跑道拐点A、B、C、D时都要停留5秒.问当甲第1次追上乙时,甲、乙各跑了多少米.
如图,有一条长方形跑道,甲从A点出发,乙从C点发.同时按逆时针方奔跑.甲速每秒6.25米,乙速每秒5米.跑道长100米,宽60米.当甲、乙每次跑道拐点A、B、C、D时都要停留5秒.问当甲第1次追上乙时,甲、乙各跑了多少米.