Question

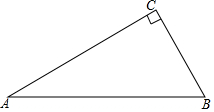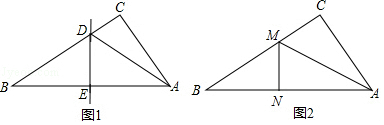
12．如图，△ABC中，∠C=90°，∠A=30°．
（1）用尺规作图作AB边上的中垂线DE，交AC于点D，交AB于点E，再结BD（保留作图痕迹，不要求写作法和证明）；
（2）在（1）题的基础上，求证：CD=DE．

Answer 1

分析 （1）直接利用线段垂直平分线的作法得出答案；
（2）直接利用中垂线的性质结合角平分线的性质得出DC=DE．

解答 （1）解：如图所示：DE就是要求作的AB边上的中垂线；

（2）证明：
∵DE是AB边上的中垂线，∠A=30°，
∴AD=BD，
∴∠ABD=∠A=30°，
∵∠C=90°，
∴∠ABC=90°-∠A=90°-30°=60°，
∴∠CBD=∠ABC-∠ABC=60°-30°=30°，
∴∠ABD=∠CBD，
∵DC⊥CB，DE⊥EB，
∴CD=DE．

点评 此题主要考查了基本作图以及线段垂直平分线的性质和角平分线的性质，正确掌握线段垂直平分线的性质是解题关键．