题目内容
1.已知抛物线的顶点为(-1,-3),与y轴的交点为(0,-5),求抛物线的解析式.求出该函数图与x轴,y轴的交点坐标.并写出增减性.分析 先利用待定系数法求二次函数的解析式,并求其与x轴的交点,即令y=0,增减性与对称轴有关,因为a=-2<0,对称轴是:x=-1,所以当x>-1时,y随x的增大而减小,当x<-1时,y随x的增大而增大.
解答 解:∵抛物线的顶点为(-1,-3),
设抛物线的解析式为:y=a(x+1)2-3,
把(0,-5)代入得:-5=a(0+1)2-3,
a=-2,
∴抛物线的解析式为:y=-2(x+1)2-3,
当y=0时,-2(x+1)2-3=0,
(x+1)2=-$\frac{3}{2}$,
此方程无解,
则抛物线与x轴无交点,与y轴的交点为(0,-5),
当x>-1时,y随x的增大而减小,
当x<-1时,y随x的增大而增大.
点评 本题考查了利用待定系数法求二次函数的解析式及二次函数的性质,明确求与x轴的交点时,令y=0;求与y轴的交点时,令x=0;抛物线的增减性与对称轴有关:①当a>0时,对称轴的左侧,y随x的增大而减小,对称轴的右侧,y随x的增大而增大.②当a<0时,对称轴的左侧,y随x的增大而增大,对称轴的右侧,y随x的增大而减小.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
12.已知二次函数y=-$\frac{1}{2}$x2-3x-$\frac{5}{2}$,设自变量的值分别为x1,x2,x3,且-3<x1<x2<x3,则对应的函数值y1,y2,y3的大小关系是( )
| A. | y1>y2>y3 | B. | y1<y2<y3 | C. | y2>y3>y1 | D. | y2<y3<y1 |
6.已知方程x2+bx+c=0有两个相等的实数根,且当x=a与x=a+n时,x2+bx+c=m,则m、n的关系为( )
| A. | m=$\frac{1}{2}$n | B. | m=$\frac{1}{4}$n | C. | m=$\frac{1}{2}$n2 | D. | m=$\frac{1}{4}$n2 |
11.若多项式a(a-3)x2-ax+3x-5是关于x的一次多项式,则a的取值是( )
| A. | 0 | B. | 3 | C. | 0或3 | D. | 无法确定 |
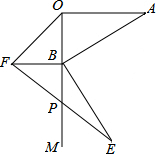 如图,AO⊥OM,OA=8$\sqrt{2}$,点B为射线OM上的一个动点,分别以OB,AB为直角边,B为直角顶点,在OM两侧作等腰Rt△OBF、等腰Rt△ABE,连接EF交OM于P点,当点B在射线OM上移动时,PB的长度为4$\sqrt{2}$.
如图,AO⊥OM,OA=8$\sqrt{2}$,点B为射线OM上的一个动点,分别以OB,AB为直角边,B为直角顶点,在OM两侧作等腰Rt△OBF、等腰Rt△ABE,连接EF交OM于P点,当点B在射线OM上移动时,PB的长度为4$\sqrt{2}$.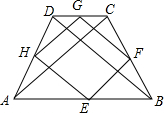 四边形ABCD中,DC∥AB,AC⊥BD,AC=BD,E、F、G、H分别是AB、BC、CD、DA的中点.
四边形ABCD中,DC∥AB,AC⊥BD,AC=BD,E、F、G、H分别是AB、BC、CD、DA的中点.