题目内容
9.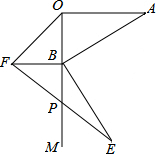 如图,AO⊥OM,OA=8$\sqrt{2}$,点B为射线OM上的一个动点,分别以OB,AB为直角边,B为直角顶点,在OM两侧作等腰Rt△OBF、等腰Rt△ABE,连接EF交OM于P点,当点B在射线OM上移动时,PB的长度为4$\sqrt{2}$.
如图,AO⊥OM,OA=8$\sqrt{2}$,点B为射线OM上的一个动点,分别以OB,AB为直角边,B为直角顶点,在OM两侧作等腰Rt△OBF、等腰Rt△ABE,连接EF交OM于P点,当点B在射线OM上移动时,PB的长度为4$\sqrt{2}$.
分析 过E作EM⊥OP于M,首先证明△ABO≌△BEN,得到BO=ME;进而证明△BPF≌△MPE,即可解决问题.
解答 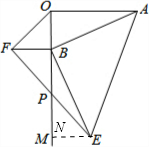 解:如图,过点E作EN⊥BM,垂足为点N;
解:如图,过点E作EN⊥BM,垂足为点N;
∵∠AOB=∠ABE=∠BME=90°,
∴∠ABO+∠BAO=∠ABO+∠MBE,
∴∠BAO=∠MBE;
∵△ABE、△BFO均为等腰直角三角形,
∴AB=BE,BF=BO;
在△ABO与△BEN中,
$\left\{\begin{array}{l}{∠BAO=∠MBE}\\{∠AOB=∠BME}\\{AB=BE}\end{array}\right.$,
∴△ABO≌△BEN(AAS),
∴BO=ME,BM=AO;而BO=BF,
∴BF=ME;
在△BPF与△MPE中,
$\left\{\begin{array}{l}{∠FBP=∠EMP}\\{∠FPB=∠EPM}\\{BF=ME}\end{array}\right.$,
∴△BPF≌△MPE(AAS),
∴BP=MP=$\frac{1}{2}$;而BM=AO,
∴BP=$\frac{1}{2}$AO=$\frac{1}{2}$×8$\sqrt{2}$=4$\sqrt{2}$,
故答案为:4$\sqrt{2}$.
点评 本题考查了三角形内角和定理,全等三角形的性质和判定的应用,解题的关键是作辅助线,构造全等三角形,灵活运用有关定理来分析或解答.

练习册系列答案
相关题目
18.如果点A(m-2,2m)在第一、三象限的角平分线上,那么点N(-m+2,m-1)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
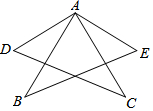 如图,AB=AC,AD=AE,CD=BE.请问∠DAB与∠EAC相等吗?请说明理由.
如图,AB=AC,AD=AE,CD=BE.请问∠DAB与∠EAC相等吗?请说明理由. 如图,点A的坐标为(8,0),点B为y轴的负半轴上的一个动点,分别以OB,AB为直角边在第三、第四象限作等腰Rt△OBF、等腰Rt△ABE,连接EF交y轴于P点,当点B在y轴上移动时,PB的长度为4.
如图,点A的坐标为(8,0),点B为y轴的负半轴上的一个动点,分别以OB,AB为直角边在第三、第四象限作等腰Rt△OBF、等腰Rt△ABE,连接EF交y轴于P点,当点B在y轴上移动时,PB的长度为4.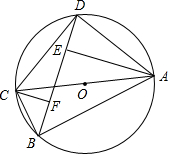 如图,四边形ABCD为⊙O的内接四边形,AC为⊙O直径,AE⊥BD于E,CF⊥BD于F.
如图,四边形ABCD为⊙O的内接四边形,AC为⊙O直径,AE⊥BD于E,CF⊥BD于F.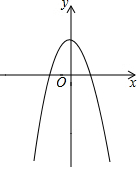 如图,已知二次函数y=-x2+c的图象经过点A(-2,0).
如图,已知二次函数y=-x2+c的图象经过点A(-2,0).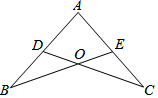 已知(如图):点D,E分别在AB,AC上,BE,CD交于O,且AB=AC,∠B=∠C.
已知(如图):点D,E分别在AB,AC上,BE,CD交于O,且AB=AC,∠B=∠C.