Question

16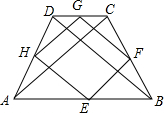．四边形ABCD中，DC∥AB，AC⊥BD，AC=BD，E、F、G、H分别是AB、BC、CD、DA的中点．
（1）四边形EFGH是什么特殊的四边形？请说明你的理由；
（2）若AB=6，DC=2，求四边形EFGH的边长．

Answer 1

分析 （1）先由三角形的中位线定理求出四边相等，然后由AC⊥BD入手，进行正方形的判定；
（2）连接HF，利用梯形的中位线定理求出HF的长，然后结合（1）的结论，求出EH²=2，即可得出正方形EHGF的边长．

解答 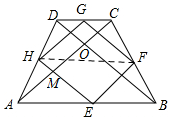解：（1）四边形EFGH是正方形．
理由：∵在△ABC中，E、F分别是AB、BC的中点，
∴EF=$\frac{1}{2}$AC，
同理FG=$\frac{1}{2}$BD，GH=$\frac{1}{2}$AC，HE=$\frac{1}{2}$BD，
∵在梯形ABCD中，AC=BD，
∴EF=FG=GH=HE，
∴四边形EFGH为菱形．      
设AC与EH交于点M，AC与BD交于点O，
∵在△ABD中，E、H分别是AB、AD的中点，
∴EH∥BD，同理GH∥AC
又∵AC⊥BD，
∴∠BOC=90°．
∴∠EHG=∠EMC=∠BOC=90°
∴菱形EFGH为正方形；

（2）如图，连接HF，在梯形ABCD中，
∵H、F分别是AD、BC的中点，
∴HF=$\frac{1}{2}$（AB+DC）=$\frac{1}{2}$（6+2）=4，
在Rt△HEF中，EG²=EH²+HG²，
即16=2EH²，
∴EH²=8，
即EH=$2\sqrt{2}$，
∴四边形EFGH的边长为2$\sqrt{2}$．

点评 此题主要考查了等腰梯形的性质及三角形、梯形的中位线定理以及勾股定理的综合应用，解答本题的关键是根据三角形的中位线定理得出EH=HG=GF=FE，这是本题的突破口．