题目内容
6.已知方程x2+bx+c=0有两个相等的实数根,且当x=a与x=a+n时,x2+bx+c=m,则m、n的关系为( )| A. | m=$\frac{1}{2}$n | B. | m=$\frac{1}{4}$n | C. | m=$\frac{1}{2}$n2 | D. | m=$\frac{1}{4}$n2 |
分析 根据根的判别式可得△=b2-4c=0即c=$\frac{1}{4}$b2 ①,由题意知x=a和x=a+n是方程x2+bx+c-m=0的两根,根据韦达定理可得a+a+n=-b即b=-(2a+n)②、a(a+n)=c-m ③,
将①、②代入③整理可得答案.
解答 解:∵方程x2+bx+c=0有两个相等的实数根,
∴△=b2-4c=0,即c=$\frac{1}{4}$b2 ①,
∵当x=a与x=a+n时,x2+bx+c=m,
即x=a和x=a+n是方程x2+bx+c-m=0的两根,
∴a+a+n=-b,即b=-(2a+n)②,
a(a+n)=c-m ③,
将①、②代入③可得:a2+an=$\frac{1}{4}$[-(2a+n)]2-m,
整理可得m=$\frac{1}{4}$n2,
故选:D.
点评 本题主要考查一元二次方程根的判别式和韦达定理,熟练掌握一元二次方程的根与判别式的关系及其与系数的关系是解题的关键.

练习册系列答案
相关题目
16. 如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:
如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:
①BE=$\frac{1}{2}$GE;
②△AGE≌△ECF;
③∠FCD=45°
其中,正确的结论有( )
 如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:
如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:①BE=$\frac{1}{2}$GE;
②△AGE≌△ECF;
③∠FCD=45°
其中,正确的结论有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
11.已知y是x的二次函数,函数y与自变量x的对应值如表:
该二次函数图象向左平移3个单位,图象经过原点.
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
18.如果点A(m-2,2m)在第一、三象限的角平分线上,那么点N(-m+2,m-1)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
16.已知二次函数y=3(x-m)2+m+1的顶点在第二象限,则m的取值范围是( )
| A. | m>0 | B. | m<-1 | C. | -1<m<0 | D. | m>-1 |
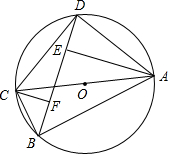 如图,四边形ABCD为⊙O的内接四边形,AC为⊙O直径,AE⊥BD于E,CF⊥BD于F.
如图,四边形ABCD为⊙O的内接四边形,AC为⊙O直径,AE⊥BD于E,CF⊥BD于F.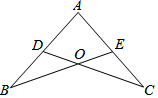 已知(如图):点D,E分别在AB,AC上,BE,CD交于O,且AB=AC,∠B=∠C.
已知(如图):点D,E分别在AB,AC上,BE,CD交于O,且AB=AC,∠B=∠C.