题目内容
7.已知直线kx+(k+1)y-1=0(k为正整数)与坐标轴所构成的直角三角形的面积为Sk(k=1,2,3,…,2006),则S1+S2+S3+…+S2006=$\frac{1003}{2007}$.分析 由于直线kx+(k+1)y-1=0(k为正整数),可以分别确定直线与坐标轴的两个交点坐标,然后利用坐标即可确定与坐标轴所构成的直角三角形的面积,然后根据面积即可求出S1+S2+S3+S4+…+S2005+S2006的值.
解答 解:∵直线kx+(k+1)y-1=0(k为正整数),
当x=0时,y=$\frac{1}{k+1}$,
当y=0时,x=$\frac{1}{k}$,
∴S1+S2+S3+S4+…+S2005+S2006=$\frac{1}{2}(\frac{1}{1×2}+\frac{1}{2×3}+…+\frac{1}{2006×2007})=\frac{1}{2}(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+..+\frac{1}{2006}-\frac{1}{2007})$=$\frac{1003}{2007}$.
故答案$\frac{1003}{2007}$
点评 此题主要考查一次函数与坐标轴所围成的直角三角形的面积问题,数学根据解析式求出与坐标轴的交点坐标,然后利用坐标表示相关的线段的长度,然后利用三角形的面积即可解决问题.

练习册系列答案
相关题目
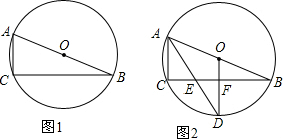
 如图,点O为$\widehat{BC}$所在圆的圆心,∠BOC=112°,点D在BA的延长线上,AD=AC,则∠D=28°.
如图,点O为$\widehat{BC}$所在圆的圆心,∠BOC=112°,点D在BA的延长线上,AD=AC,则∠D=28°.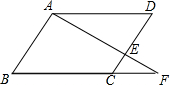 如图,?ABCD中,∠B=60°,过A作BA的垂线交CD于点E,交BC的延长线于点F,若S△CEF=9$\sqrt{3}$,求EF的长.
如图,?ABCD中,∠B=60°,过A作BA的垂线交CD于点E,交BC的延长线于点F,若S△CEF=9$\sqrt{3}$,求EF的长. 如图,在Rt△ABC中,∠BAC=90°,∠ABC的平分线BD交AC于点D,DE是BC的垂直平分线,点E是垂足.已知DC=8,AD=4,则图中长为4$\sqrt{3}$的线段有( )
如图,在Rt△ABC中,∠BAC=90°,∠ABC的平分线BD交AC于点D,DE是BC的垂直平分线,点E是垂足.已知DC=8,AD=4,则图中长为4$\sqrt{3}$的线段有( )