题目内容
15.已知$\sqrt{\frac{x-6}{9-x}}$=$\frac{\sqrt{x-6}}{\sqrt{x-5}}$,且x为奇数,求(1+x)$\sqrt{\frac{{x}^{2}-5x+4}{{x}^{2}-1}}$的值.分析 根据已知求出x的值,把x的值代入所求的代数式计算得到答案.
解答 解:∵$\sqrt{\frac{x-6}{9-x}}$=$\frac{\sqrt{x-6}}{\sqrt{x-5}}$,
∴9-x=x-5,解得,x=7,符合x为奇数,
(1+x)$\sqrt{\frac{{x}^{2}-5x+4}{{x}^{2}-1}}$=$\frac{7}{4}\sqrt{6}$.
点评 本题考查的是二次根式的化简求值,正确化简二次根式求出x的值是解题的关键.

练习册系列答案
相关题目
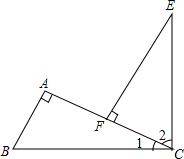 如图,∠A=90°,BC⊥EC,EF⊥AC,BC=CE,你能根据以上的条件,说明△ABC≌△FCE吗?
如图,∠A=90°,BC⊥EC,EF⊥AC,BC=CE,你能根据以上的条件,说明△ABC≌△FCE吗?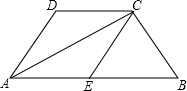 如图,梯形ABCD中,AB∥DC,AC平分∠BAD,CE∥DA交AB于点E.求证:四边形ADCE是菱形.
如图,梯形ABCD中,AB∥DC,AC平分∠BAD,CE∥DA交AB于点E.求证:四边形ADCE是菱形.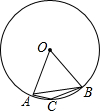 如图,点A,B,C是⊙O上的点,AO=AB,则∠ACB=150度.
如图,点A,B,C是⊙O上的点,AO=AB,则∠ACB=150度.