题目内容
11.在平面直角坐标系中,点A从原点O出发,按下平移、斜上、上平移、斜下的方向依次不断移动,每次移动一个单位,其移动路线如图所示,已知点A2的纵坐标为$\frac{\sqrt{2}}{2}$,则点A4n(n是正整数)的横坐标为(2+$\sqrt{2}$)n.(用n的代数式表示)
分析 先根据勾股定理求得AH=$\sqrt{{A}_{1}{{A}_{2}}^{2}-{A}_{2}{H}^{2}}$=$\frac{\sqrt{2}}{2}$,从而得出A1(1,0)、A2(1+$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$)、A3(2+$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$)、A4(2+$\sqrt{2}$,0),即可知每向前平移四次即前进2+$\sqrt{2}$个单位,据此知A8[2(2+$\sqrt{2}$)0,]、A12[3(2+$\sqrt{2}$),0],…,从而得出答案.
解答 解:如图,过点A2作A2H⊥x轴于点H,
由题意知,A2H=$\frac{\sqrt{2}}{2}$,A1A2=1,
则AH=$\sqrt{{A}_{1}{{A}_{2}}^{2}-{A}_{2}{H}^{2}}$=$\sqrt{{1}^{2}-(\frac{\sqrt{2}}{2})^{2}}$=$\frac{\sqrt{2}}{2}$,
则A1(1,0)、A2(1+$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$)、A3(2+$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$)、A4(2+$\sqrt{2}$,0),
A8[2(2+$\sqrt{2}$)0,]、A12[3(2+$\sqrt{2}$),0],…
∴A4n[(2+$\sqrt{2}$)n,0],
故答案为:(2+$\sqrt{2}$)n.
点评 本题主要考查平移的情形下坐标的变化特点,仔细观察图形,分别求出n=1、2、3时对应的点A4n的对应的坐标是解题的关键.

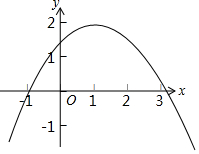 如图为二次函数y=ax2+bx+c的图象,则下列说法正确的是( )
如图为二次函数y=ax2+bx+c的图象,则下列说法正确的是( )| A. | abc>0 | B. | 3a-b+c>0 | C. | 2a+b+c>0 | D. | c>-4a |
 如图,已知图中大圆的直径为m,则阴影部分的面积为$\frac{π{m}^{2}}{8}$.(用含m的代数式表示,并化简)
如图,已知图中大圆的直径为m,则阴影部分的面积为$\frac{π{m}^{2}}{8}$.(用含m的代数式表示,并化简)