题目内容
16.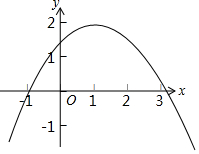 如图为二次函数y=ax2+bx+c的图象,则下列说法正确的是( )
如图为二次函数y=ax2+bx+c的图象,则下列说法正确的是( )| A. | abc>0 | B. | 3a-b+c>0 | C. | 2a+b+c>0 | D. | c>-4a |
分析 由抛物线的开口方向、对称轴位置及图象与y轴交点可判断A;由a<0及x=-1时y=a-b+c<0可得2a+a-b+c<0,即可判断B;由-$\frac{b}{2a}>1$知b>-2a,即2a+b>0,结合c>0可判断C;根据y=ax2+bx+c与x轴的两个交点的横坐标x1=-1、x2>3,可知x1•x2=$\frac{c}{a}$<-3,从而判断D.
解答 解:由函数图象可知,
a<0,b>0,c>0,
∴abc<0,故选项A错误;
当x=-1时,y=a-b+c<0,由a<0,
∴3a-b+c<0,故选项B错误;
∵-$\frac{b}{2a}>1$,a<0,b>0,c>0,
∴b>-2a,
∴2a+b+c>0,故选项C正确;
由函数图象可知,抛物线y=ax2+bx+c与x轴的两个交点的横坐标x1=-1,x2>3,
∴x1•x2=$\frac{c}{a}$<-3,
∵a<0,
∴c>-3a,故选项D错误;
故选:C.
点评 本题主要考查二次函数的图象与系数的关系,熟练将二次函数图象的开口方向、对称轴、顶点坐标、与坐标轴的交点及函数图象上的特殊点等有关信息转化成与系数有关的式子时解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
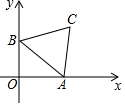 如图,点A,B分别是x轴.y轴上的两个动点,以AB为边作等边△ABC,若AB=2,设点C到原点O的距离为d,则d的取值范围是$\sqrt{3}$-1≤d≤$\sqrt{3}$+1.
如图,点A,B分别是x轴.y轴上的两个动点,以AB为边作等边△ABC,若AB=2,设点C到原点O的距离为d,则d的取值范围是$\sqrt{3}$-1≤d≤$\sqrt{3}$+1.
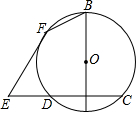 如图,AB是⊙O的直径,$\widehat{AC}$=$\widehat{AD}$,E为弦CD的延长线上一点,EF与⊙O相切于F,若∠E=40°,则∠EFB的度数为160°.
如图,AB是⊙O的直径,$\widehat{AC}$=$\widehat{AD}$,E为弦CD的延长线上一点,EF与⊙O相切于F,若∠E=40°,则∠EFB的度数为160°.