题目内容
 如图,圆⊙O的半径为1,等腰直角三角形ABC的顶点B的坐标为(2,0),∠CAB=90°,AC=AB,顶点A在⊙O上运动.
如图,圆⊙O的半径为1,等腰直角三角形ABC的顶点B的坐标为(2,0),∠CAB=90°,AC=AB,顶点A在⊙O上运动.(1)当点A运动到x轴的负半轴上时,试判断直线BC与⊙O的位置关系,并说明理由.
(2)当直线AB与⊙O相切时,求A点的坐标.
考点:直线与圆的位置关系,切线的性质
专题:
分析:(1)根据题意过点O作OM⊥BC于点M,求出OM的长,与半径比较得出位置关系.
(2)相切时有两种情况,在第一象限或者第四象限,连接OA,并过点A作AE⊥OB于点E,在Rt△OAE中求出OE,然后就能求出A点坐标.
(2)相切时有两种情况,在第一象限或者第四象限,连接OA,并过点A作AE⊥OB于点E,在Rt△OAE中求出OE,然后就能求出A点坐标.
解答: 解:(1)直线BC与⊙O相切;
解:(1)直线BC与⊙O相切;
如图1,过点O作OM⊥BC于点M,
∴∠OBM=∠BOM=45°,
∴OM=OB•sin45°=
,
∵⊙O的半径为1,
∴直线BC与⊙O相离;
(2)①当点A位于第一象限时(如右图2):
连接OA,并过点A作AE⊥OB于点E,
∵直线AB与⊙O相切,
 ∴∠OAB=90°,
∴∠OAB=90°,
又∵∠CAB=90°,
∴∠CAB+∠OAB=180°,
∴点O、A、C在同一条直线上
∴∠AOB=∠C=45°,即∠CBO=90°,
在Rt△OAE中,OE=AE=
OB=1.
点A的坐标为(1,1);
 ②当点A位于第四象限时(如右图3):
②当点A位于第四象限时(如右图3):
过点作AE⊥BC于点E,
∵AB是切线,
∴OA⊥AB,
∵∠OAB=90°,
∴点O与点C重合,
∴点A的坐标为(1,-1).
 解:(1)直线BC与⊙O相切;
解:(1)直线BC与⊙O相切;如图1,过点O作OM⊥BC于点M,
∴∠OBM=∠BOM=45°,
∴OM=OB•sin45°=
| 2 |
∵⊙O的半径为1,
∴直线BC与⊙O相离;
(2)①当点A位于第一象限时(如右图2):
连接OA,并过点A作AE⊥OB于点E,
∵直线AB与⊙O相切,
 ∴∠OAB=90°,
∴∠OAB=90°,又∵∠CAB=90°,
∴∠CAB+∠OAB=180°,
∴点O、A、C在同一条直线上
∴∠AOB=∠C=45°,即∠CBO=90°,
在Rt△OAE中,OE=AE=
| 1 |
| 2 |
点A的坐标为(1,1);
 ②当点A位于第四象限时(如右图3):
②当点A位于第四象限时(如右图3):过点作AE⊥BC于点E,
∵AB是切线,
∴OA⊥AB,
∵∠OAB=90°,
∴点O与点C重合,
∴点A的坐标为(1,-1).
点评:此题考查了切线的性质与判定、直线与圆的位置关系、等腰直角三角形的性质以及待定系数法求一次函数解析式等知识.此题难度较大,注意掌握辅助线的作法,注意掌握方程思想、分类讨论思想与数形结合思想的应用.

练习册系列答案
相关题目
在平面直角坐标系中,以点(0,2)为圆心,2为半径的圆与x轴的位置关系( )
| A、相离 | B、相交 | C、相切 | D、不确定 |
在△ABC中,AB=AC,若AC的垂直平分线DE交AC于点D,交BC于点E,且∠BAE=90°,则∠B为( )
| A、60° | B、30° |
| C、45° | D、无法确定 |
 如图,∠A=55°,∠B=30°,∠C=35°,求∠BDC的度数.
如图,∠A=55°,∠B=30°,∠C=35°,求∠BDC的度数.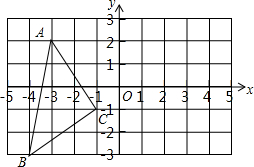 如图,在平面直角坐标系中,A(-3,2),B(-4,-3),C(-1,-1).
如图,在平面直角坐标系中,A(-3,2),B(-4,-3),C(-1,-1).