题目内容
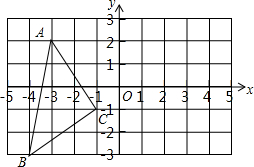 如图,在平面直角坐标系中,A(-3,2),B(-4,-3),C(-1,-1).
如图,在平面直角坐标系中,A(-3,2),B(-4,-3),C(-1,-1).(1)在图中作出△ABC关于y轴对称的△A1B1C1;
(2)写出点△A1,B1,C1的坐标(直接写答案):A1
(3)△A1B1C1的面积为
(4)在y轴上画出点P,使PB+PC最小.
考点:作图-轴对称变换,轴对称-最短路线问题
专题:
分析:(1)根据关于y轴对称点的性质得出各对应点位置进而得出答案;
(2)利用(1)中作画图形,进而得出各点坐标;
(3)利用△ABC所在矩形面积减去△ABC周围三角形面积进而求出即可;
(4)利用轴对称求最短路径的方法得出答案.
(2)利用(1)中作画图形,进而得出各点坐标;
(3)利用△ABC所在矩形面积减去△ABC周围三角形面积进而求出即可;
(4)利用轴对称求最短路径的方法得出答案.
解答: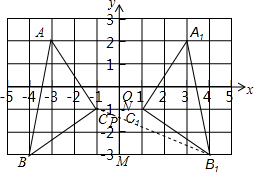 解:(1)如图所示:△A1B1C1,即为所求;
解:(1)如图所示:△A1B1C1,即为所求;
(2)A1 (3,2);B1 (4,-3);C1 (1,-1);
故答案为:(3,2);(4,-3);(1,-1);
(3)△A1B1C1的面积为:3×5-
×2×3-
×1×5-
×2×3=6.5;
(4)如图所示:P点即为所求.
 解:(1)如图所示:△A1B1C1,即为所求;
解:(1)如图所示:△A1B1C1,即为所求;(2)A1 (3,2);B1 (4,-3);C1 (1,-1);
故答案为:(3,2);(4,-3);(1,-1);
(3)△A1B1C1的面积为:3×5-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(4)如图所示:P点即为所求.
点评:此题主要考查了轴对称变换以及三角形面积求法等知识,正确利用轴对称图形的性质得出是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数y=(m+1)x-(4m-3)的图象在第一、二、三象限,那么m的取值范围是( )
A、m<
| ||
B、-1<m<
| ||
| C、m<-1 | ||
| D、m>-1 |
已知一矩形的两边长分别为7cm和12cm,其中一个内角的平分线分长边为两部分,这两部分的长分别为( )
| A、6cm和6cm |
| B、7cm和5cm |
| C、4cm和8cm |
| D、3cm和9cm |
 如图,圆⊙O的半径为1,等腰直角三角形ABC的顶点B的坐标为(2,0),∠CAB=90°,AC=AB,顶点A在⊙O上运动.
如图,圆⊙O的半径为1,等腰直角三角形ABC的顶点B的坐标为(2,0),∠CAB=90°,AC=AB,顶点A在⊙O上运动.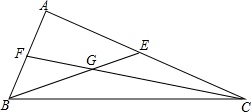 如图,△ABC的中线BE、CF相交于G,且AB=12,AC=16,BC=20,求GC的长.
如图,△ABC的中线BE、CF相交于G,且AB=12,AC=16,BC=20,求GC的长. 如图,△ABC中,∠ACB=90°,以AB、BC为边长所作的正方形面积分别为400、256,则以AC为边长所作的正方形面积等于
如图,△ABC中,∠ACB=90°,以AB、BC为边长所作的正方形面积分别为400、256,则以AC为边长所作的正方形面积等于