题目内容
12.下列式子中,字母x的取值范围是x>2的式子是( )| A. | y=$\sqrt{x-2}$ | B. | y=$\frac{1}{\sqrt{x-2}}$ | C. | y=$\sqrt{2x-1}$ | D. | y=$\frac{1}{\sqrt{2x-1}}$ |
分析 可以分别求出选项中的四个式子,使得它们有意义的x取值范围,从而可以得到符合题目要求的选项.
解答 解:A.$y=\sqrt{x-2}$要有意义,则x-2≥0,得x≥2;
B.$y=\frac{1}{\sqrt{x-2}}$要有意义,则$\left\{\begin{array}{l}{x-2≥0}\\{x-2≠0}\end{array}\right.$,得x>2;
C.$y=\sqrt{2x-1}$要有意义,则2x-1≥0,得x≥$\frac{1}{2}$;
D.$y=\frac{1}{\sqrt{2x-1}}$要有意义,则$\left\{\begin{array}{l}{2x-1≥0}\\{2x-1≠0}\end{array}\right.$,得$x>\frac{1}{2}$;
故选B.
点评 本题考查二次根式有意义和分式有意义的条件,解题的关键是根据题目可以得到在x取什么值时,使得原式有意义.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
5.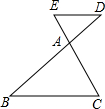 如图,已知点D、E分别在△ABC的边BA、CA的延长上,下列给出的条件中,不能判定DE∥BC的是( )
如图,已知点D、E分别在△ABC的边BA、CA的延长上,下列给出的条件中,不能判定DE∥BC的是( )
 如图,已知点D、E分别在△ABC的边BA、CA的延长上,下列给出的条件中,不能判定DE∥BC的是( )
如图,已知点D、E分别在△ABC的边BA、CA的延长上,下列给出的条件中,不能判定DE∥BC的是( )| A. | BD:AB=CE:AC | B. | DE:BC=AB:AD | C. | AB:AC=AD:AE | D. | AD:DB=AE:EC |
4. 如图,在△AOB中,∠BOA=90°,∠BOA的两边分别与函数$y=-\frac{1}{x}$、$y=\frac{2}{x}$的图象交于B、A两点,若$AB=\sqrt{6}$,则AO的值为( )
如图,在△AOB中,∠BOA=90°,∠BOA的两边分别与函数$y=-\frac{1}{x}$、$y=\frac{2}{x}$的图象交于B、A两点,若$AB=\sqrt{6}$,则AO的值为( )
 如图,在△AOB中,∠BOA=90°,∠BOA的两边分别与函数$y=-\frac{1}{x}$、$y=\frac{2}{x}$的图象交于B、A两点,若$AB=\sqrt{6}$,则AO的值为( )
如图,在△AOB中,∠BOA=90°,∠BOA的两边分别与函数$y=-\frac{1}{x}$、$y=\frac{2}{x}$的图象交于B、A两点,若$AB=\sqrt{6}$,则AO的值为( )| A. | $\frac{3}{2}\sqrt{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |

 等边△ABC高为7$\sqrt{3}$,边长为14.BD为AC边上高,P是BD上的动点,且E是BC上-点,BE=CE,则△PEC的周长最小值为7$\sqrt{3}$+7.
等边△ABC高为7$\sqrt{3}$,边长为14.BD为AC边上高,P是BD上的动点,且E是BC上-点,BE=CE,则△PEC的周长最小值为7$\sqrt{3}$+7.