题目内容
4.有一次课外活动课中,罗纳用木棒制作了一个三角形,已知它的边长分别为$\sqrt{8}$cm,$\sqrt{12}$cm,$\sqrt{18}$cm,则它的周长为(5$\sqrt{2}+2\sqrt{3}$)cm.分析 根据罗纳用木棒制作了一个三角形,已知它的边长分别为$\sqrt{8}$cm,$\sqrt{12}$cm,$\sqrt{18}$cm,可以求出该三角形的周长.
解答 解:∵罗纳用木棒制作了一个三角形,已知它的边长分别为$\sqrt{8}$cm,$\sqrt{12}$cm,$\sqrt{18}$cm,
∴此三角形的周长是:$\sqrt{8}+\sqrt{12}+\sqrt{18}$=$2\sqrt{2}+2\sqrt{3}+3\sqrt{2}=5\sqrt{2}+2\sqrt{3}$,
即它的周长是($5\sqrt{2}+2\sqrt{3}$)cm.
故答案为:(5$\sqrt{2}+2\sqrt{3}$)cm.
点评 本题考查二次根式的加减法,解题的关键是明确三角形的周长就是三边之和,要将三边的和化到最简.

练习册系列答案
相关题目
12.下列式子中,字母x的取值范围是x>2的式子是( )
| A. | y=$\sqrt{x-2}$ | B. | y=$\frac{1}{\sqrt{x-2}}$ | C. | y=$\sqrt{2x-1}$ | D. | y=$\frac{1}{\sqrt{2x-1}}$ |
2.下列计算正确的是( )
| A. | x6÷x3=x8 | B. | x3+x2=x6 | C. | (x2)3=x5 | D. | x2•x3=x5 |
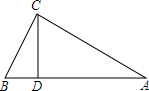 如图,△ABC中,∠C=90°,若CD⊥AB于D,且BD=4,AD=9,则CD=6.
如图,△ABC中,∠C=90°,若CD⊥AB于D,且BD=4,AD=9,则CD=6.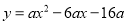 (
(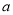 <0)与
<0)与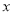 轴交于A,B两点,与y轴正半轴交于点C,且∠ACB=90°,点P是直线BC上方抛物线上的一个动点.
轴交于A,B两点,与y轴正半轴交于点C,且∠ACB=90°,点P是直线BC上方抛物线上的一个动点.