题目内容
10.函数y=$\frac{2}{\sqrt{|x|-1}}$中,自变量x的取值范围为x>1或x<-1.分析 一般地从两个角度考虑:分式的分母不为0;偶次根式被开方数大于或等于0;当一个式子中同时出现这两点时,应该是取让两个条件都满足的公共部分.
解答 解:根据题意得到:|x|-1>0,
解得|x|>1,
即x>1或x<-1,
故答案为x>1或x<-1.
点评 判断一个式子是否有意义,应考虑分母上若有字母,字母的取值不能使分母为零,二次根号下字母的取值应使被开方数为非负数.易错易混点:学生易对二次根式的非负性和分母不等于0混淆.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
12.下列式子中,字母x的取值范围是x>2的式子是( )
| A. | y=$\sqrt{x-2}$ | B. | y=$\frac{1}{\sqrt{x-2}}$ | C. | y=$\sqrt{2x-1}$ | D. | y=$\frac{1}{\sqrt{2x-1}}$ |
15.某演出小分队是由20名年龄在25岁到30岁的演员组成,请根据表格中提供的数据,(其中28岁和29岁的人数未知),试写出这20名演员年龄的众数的所有可能值26、28、29.
| 年龄(岁) | 25 | 26 | 27 | 28 | 29 | 30 |
| 人数(名) | 2 | 5 | 4 | 3 |
2.下列计算正确的是( )
| A. | x6÷x3=x8 | B. | x3+x2=x6 | C. | (x2)3=x5 | D. | x2•x3=x5 |
20.一条直线y=kx+b,其中k+b<0,kb>0,那么该直线经过( )
| A. | 第二、四象限 | B. | 第一、二、三象限 | C. | 第一、三象限 | D. | 第二、三、四象限 |
 ,则sinA=__.
,则sinA=__.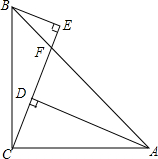 如图,AD=CE=24,BC=25,∠BCE=∠CAD,BE∥AD,BF:AF=7:24,给出下列结论:①∠E=90°;②∠BCA=90°;③∠BAC=45°;④AB=25$\sqrt{3}$.其中正确的结论有①②③.(把所有正确结论序号都填在横线上)
如图,AD=CE=24,BC=25,∠BCE=∠CAD,BE∥AD,BF:AF=7:24,给出下列结论:①∠E=90°;②∠BCA=90°;③∠BAC=45°;④AB=25$\sqrt{3}$.其中正确的结论有①②③.(把所有正确结论序号都填在横线上)