题目内容
7. 等边△ABC高为7$\sqrt{3}$,边长为14.BD为AC边上高,P是BD上的动点,且E是BC上-点,BE=CE,则△PEC的周长最小值为7$\sqrt{3}$+7.
等边△ABC高为7$\sqrt{3}$,边长为14.BD为AC边上高,P是BD上的动点,且E是BC上-点,BE=CE,则△PEC的周长最小值为7$\sqrt{3}$+7.
分析 因为CE=7是定值,要求△PEC的周长最小值,只要求得EP+CP的最小值即可,这就需考虑通过作辅助线转化EP,CP的值,从而找出其最小值求解.
解答 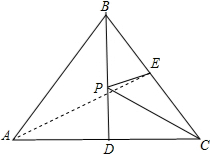 解:连接AE,与BD交于点P.
解:连接AE,与BD交于点P.
∵BD为AC边上高,
∴AD=DC,
∴BD是AC的垂直平分线,
∴A、C关于BD对称,
∴AP=CP,
∴PE+PC=PE+PA=AE,
∴AE就是EP+CP的最小值.
∵BE=CE,
∴AE是等边△ABC的高,
∴AE=7$\sqrt{3}$,
∴△PEC的周长最小值为PE+PC+EC=AE+CE=7$\sqrt{3}$+7.
故答案为7$\sqrt{3}$+7.
点评 考查等边三角形的性质和轴对称-最短路线问题,熟练掌握和运用等边三角形的性质以及轴对称的性质是本题的关键.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
20.请估计$\sqrt{10}-1$的值在( )
| A. | 1与2之间 | B. | 2与3之间 | C. | 3与4之间 | D. | 4与5之间 |
12.下列式子中,字母x的取值范围是x>2的式子是( )
| A. | y=$\sqrt{x-2}$ | B. | y=$\frac{1}{\sqrt{x-2}}$ | C. | y=$\sqrt{2x-1}$ | D. | y=$\frac{1}{\sqrt{2x-1}}$ |
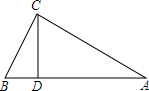 如图,△ABC中,∠C=90°,若CD⊥AB于D,且BD=4,AD=9,则CD=6.
如图,△ABC中,∠C=90°,若CD⊥AB于D,且BD=4,AD=9,则CD=6.
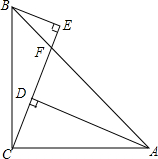 如图,AD=CE=24,BC=25,∠BCE=∠CAD,BE∥AD,BF:AF=7:24,给出下列结论:①∠E=90°;②∠BCA=90°;③∠BAC=45°;④AB=25$\sqrt{3}$.其中正确的结论有①②③.(把所有正确结论序号都填在横线上)
如图,AD=CE=24,BC=25,∠BCE=∠CAD,BE∥AD,BF:AF=7:24,给出下列结论:①∠E=90°;②∠BCA=90°;③∠BAC=45°;④AB=25$\sqrt{3}$.其中正确的结论有①②③.(把所有正确结论序号都填在横线上)