题目内容
20.如图,已知矩形ABCD中,AB=6,BC=8,E是BC边上一点(不与B、C重合),过点E作EF⊥AE交AC、CD于点M、F,过点B作BG⊥AC,垂足为G,BG交AE于点H;(1)求证:△ABH∽△ECM;
(2)设BE=x,$\frac{EH}{EM}=y$,求y关于x的函数解析式,并写出定义域;
(3)当△BHE为等腰三角形时,求BE的长.

分析 (1)由矩形的四个角为直角,得到∠ABC为直角,再由BG垂直于AC,AE垂直于EF,得到一对直角相等,利用同角的余角相等得到一对角相等,再利用外角性质得到另一对角相等,利用两角相等的三角形相似即可得证;
(2)延长BG,交AD于点K,利用两角相等的三角形相似得到三角形ABK与三角形ABC相似,由相似得比例求出AK的长,由AK与BE平行,得到三角形AHK与三角形BHE相似,表示出EH,由第一问的结论,利用相似三角形对应边成比例表示出$\frac{AH}{EM}$,即可确定出y与x的函数解析式,并求出定义域即可;
(3)当△BHE为等腰三角形时,分三种情况考虑:①当BH=BE时,利用等腰三角形的性质,角平分线定义及锐角三角函数定义求出BE的长;②当HB=HE时,利用等腰三角形的性质及锐角三角函数定义求出BE的长;③当EB=EH时,利用等腰三角形的性质及勾股定理求出BE的长即可.
解答 (1)证明:∵四边形ABCD是矩形,
∴∠ABC=90°,即∠ABG+∠CBG=90°,
∵EF⊥AE,BG⊥AC,
∴∠AEF=∠BGA=90°,
∴∠AEF=∠ABC,∠ACB+∠CBG=90°,
∴∠ABG=∠ACB,
∵∠AEC=∠ABC+∠BAE,即∠AEF+∠CEF=∠ABC+∠BAE,
∴∠BAE=∠CEF,
又∵∠ABG=∠ACB,
∴△ABH∽△ECM;
(2)解:延长BG交AD于点K,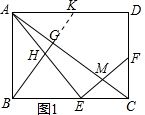
∵∠ABG=∠ACB,
又∵在矩形ABCD中,∠BAK=∠ABC=90°,
∴△ABK∽△BCA,
∴$\frac{AK}{AB}$=$\frac{AB}{BC}$,即$\frac{AK}{6}$=$\frac{6}{8}$,
∴AK=$\frac{9}{2}$,
∵在矩形ABCD中,AD∥BC,且BE=x,
∴$\frac{BE}{AK}$=$\frac{EH}{AH}$=$\frac{2x}{9}$,
∴EH=$\frac{2x}{9}$•AH,
∵△ABH∽△ECM,
∴$\frac{AH}{EM}$=$\frac{AB}{EC}$=$\frac{6}{8-x}$,
∵$\frac{EH}{EM}$=y,
∴y=$\frac{\frac{2x}{9}•AH}{EM}$=$\frac{2x}{9}$•$\frac{AH}{EM}$=$\frac{2x}{9}$•$\frac{6}{8-x}$=$\frac{4x}{24-3x}$(0<x<8);
(3)解:当△BHE为等腰三角形时,存在以下三种情况:
①当BH=BE时,则有∠BHE=∠BEH,
∵∠BHE=∠AHG,
∴∠BEH=∠AHG,
∵∠ABC=∠BGA=90°,
∴∠BEH+∠BAE=∠AHG+∠EAM=90°,
∴∠BAE=∠EAM,即AE为∠BAC的平分线,
过点E作EQ⊥AC,垂足为Q,如图2所示,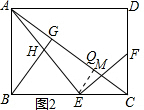
则EQ=EB=x,CE=8-x,
∵sin∠ACB=$\frac{EQ}{EC}$=$\frac{x}{8-x}$=$\frac{3}{5}$,
∴x=3,即BE=3;
②当HB=HE时,则有∠HBE=∠HEB,
∵∠ABC=∠BGC=90°,
∴∠BAE+∠HEB=∠BCG+∠HBE=90°,
∴∠BAE=∠BCG,
∴tan∠BAE=tan∠BCA=$\frac{x}{6}$=$\frac{3}{4}$,
∴x=$\frac{9}{2}$,即BE=$\frac{9}{2}$;
③当EB=EH时,则有∠EHB=∠EBH,
又∵∠EHB=∠AHG,
∴∠AHG=∠EBH,
∵∠BGA=∠BGC=90°,
∴∠CAE+∠AHG=∠BCG+∠EBH=90°,
∴∠CAE=∠BCG,
∴EA=EC=8-x,
∵在Rt△ABE中,AB2+BE2=AE2,即62+x2=(8-x)2,
解得:x=$\frac{7}{4}$,即BE=$\frac{7}{4}$,
综上所述,当△BHE是等腰三角形时,BE的长为3或$\frac{9}{2}$或$\frac{7}{4}$.
点评 此题属于相似形综合题,涉及的知识有:矩形的性质,相似三角形的判定与性质,平行线等分线段定理,勾股定理,锐角三角函数定义,以及等腰三角形的性质,熟练掌握相似三角形的判定与性质是解本题的关键.

 名校课堂系列答案
名校课堂系列答案 如图,数轴上点P表示的数可能是( )
如图,数轴上点P表示的数可能是( )| A. | $-\sqrt{5}$ | B. | $\sqrt{5}$ | C. | -3.8 | D. | $-\sqrt{10}$ |
| A. | y=$\sqrt{x-2}$ | B. | y=$\frac{1}{\sqrt{x-2}}$ | C. | y=$\sqrt{2x-1}$ | D. | y=$\frac{1}{\sqrt{2x-1}}$ |
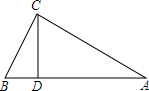 如图,△ABC中,∠C=90°,若CD⊥AB于D,且BD=4,AD=9,则CD=6.
如图,△ABC中,∠C=90°,若CD⊥AB于D,且BD=4,AD=9,则CD=6.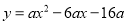 (
(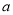 <0)与
<0)与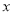 轴交于A,B两点,与y轴正半轴交于点C,且∠ACB=90°,点P是直线BC上方抛物线上的一个动点.
轴交于A,B两点,与y轴正半轴交于点C,且∠ACB=90°,点P是直线BC上方抛物线上的一个动点.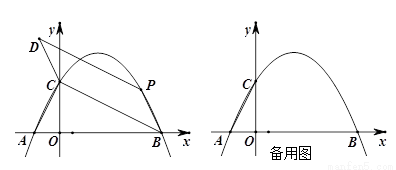
 ,则sinA=__.
,则sinA=__.