题目内容
17.a、b、c、d为互不相等的四个有理数,且c=3,|a-c|=|b-c|=|d-b|=1,则|a-d|的值是多少?分析 根据题意分别求出a、b的值,根据绝对值的性质分别计算即可.
解答 解:∵a、b、c、d为互不相等的四个有理数,且c=3,|a-c|=|b-c|=1,
∴a=2,b=4或a=4,b=2,
当a=2,b=4,|d-b|=1时,
d=3或5,又c=3,
∴d=5,则|a-d|=2,
当a=4,b=2,|d-b|=1时,
d=3或1,又c=3,
∴d=1,则|a-d|=3,
∴|a-d|=3.
点评 本题考查的是绝对值的概念和性质,掌握绝对值等于一个正数的数有两个,绝对值等于0的数有一个,没有绝对值等于负数的数是解题的关键,注意分情况讨论思想的正确运用.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
12.下列式子中,字母x的取值范围是x>2的式子是( )
| A. | y=$\sqrt{x-2}$ | B. | y=$\frac{1}{\sqrt{x-2}}$ | C. | y=$\sqrt{2x-1}$ | D. | y=$\frac{1}{\sqrt{2x-1}}$ |
15.某演出小分队是由20名年龄在25岁到30岁的演员组成,请根据表格中提供的数据,(其中28岁和29岁的人数未知),试写出这20名演员年龄的众数的所有可能值26、28、29.
| 年龄(岁) | 25 | 26 | 27 | 28 | 29 | 30 |
| 人数(名) | 2 | 5 | 4 | 3 |
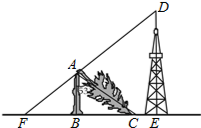 如图,一棵大树在一次强台风中折断倒下,未折断树杆AB与地面仍保持垂直的关系,而折断部分AC与未折断树杆AB形成53°的夹角.树杆AB旁有一座与地面垂直的铁塔DE,测得BE=6米,塔高DE=9米.在某一时刻的太阳照射下,未折断树杆AB落在地面的影子FB长为4米,且点F、B、C、E在同一条直线上,点F、A、D也在同一条直线上.求这棵大树没有折断前的高度.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33)
如图,一棵大树在一次强台风中折断倒下,未折断树杆AB与地面仍保持垂直的关系,而折断部分AC与未折断树杆AB形成53°的夹角.树杆AB旁有一座与地面垂直的铁塔DE,测得BE=6米,塔高DE=9米.在某一时刻的太阳照射下,未折断树杆AB落在地面的影子FB长为4米,且点F、B、C、E在同一条直线上,点F、A、D也在同一条直线上.求这棵大树没有折断前的高度.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33)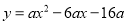 (
(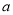 <0)与
<0)与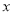 轴交于A,B两点,与y轴正半轴交于点C,且∠ACB=90°,点P是直线BC上方抛物线上的一个动点.
轴交于A,B两点,与y轴正半轴交于点C,且∠ACB=90°,点P是直线BC上方抛物线上的一个动点.