题目内容
4.如图,B,D是反比例函数图象上两点,过B,D作x轴垂线,垂足分别为A,C,连接OD交AB于点E,若∠BOA=60°,OD是∠BOA的平分线,四边形ACDE的面积为$\sqrt{2}$.试写出反比例函数在第一象限内的解析式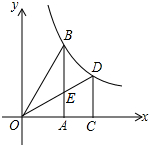 y=$\frac{3\sqrt{2}}{x}$.
y=$\frac{3\sqrt{2}}{x}$.
分析 根据反比例系数的几何意义知S△BOE=S四边形ACDE=$\sqrt{2}$,设B坐标为(x,$\frac{k}{x}$),由AB=OA•tan∠BOA知k=$\sqrt{3}$x2,根据S△BOE=S△AOB-S△AOE列出关于x的方程得x2,从而得知k的值.
解答 解:设反比例函数解析式为y=$\frac{k}{x}$(k>0),
∵S△AOB=S△COD=$\frac{1}{2}$k,即S△AOE+S△BOE=S△AOE+S四边形ACDE,
∴S△BOE=S四边形ACDE=$\sqrt{2}$,
设点B坐标为(x,$\frac{k}{x}$),
则OA=x,AB=$\frac{k}{x}$,
∵∠BOA=60°,OD平分∠BOA,
∴∠EOA=30°,AB=OA•tan∠BOA=$\sqrt{3}$x,
∴$\sqrt{3}x=\frac{k}{x}$,即k=$\sqrt{3}$x2,
AE=OA•tan∠EOA=$\frac{\sqrt{3}}{3}x$,
∵S△BOE=S△AOB-S△AOE,
∴$\frac{1}{2}$•x•$\sqrt{3}$x-$\frac{1}{2}$•x•$\frac{\sqrt{3}}{3}$x=$\sqrt{2}$,
得:x2=$\sqrt{6}$,
则k=$\sqrt{3}$x2=3$\sqrt{2}$,
∴反比例函数的解析式为:y=$\frac{3\sqrt{2}}{x}$.
故答案为:y=$\frac{3\sqrt{2}}{x}$.
点评 本题考查了反比例函数比例系数的几何意义,解题的关键要熟记系数k与三角形的面积的关系.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
12.已知二次函数y=ax2+bx+c(a≠0)中,函数值y与自变量x的部分对应值如下表:
则关于x的一元二次方程ax2+bx+c=-2的根是x1=-4,x2=0.
| x | … | -5 | -4 | -3 | -2 | -1 | … |
| y | … | 3 | -2 | -5 | -6 | -5 | … |
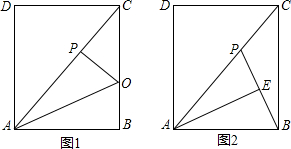
 如图,在?ABCD中,AB⊥AC,AB=1,BC=$\sqrt{5}$,对角线AC,BD交于O点,将直线AC绕点O顺时针旋转,分别交于BC,AD于点E,F.
如图,在?ABCD中,AB⊥AC,AB=1,BC=$\sqrt{5}$,对角线AC,BD交于O点,将直线AC绕点O顺时针旋转,分别交于BC,AD于点E,F.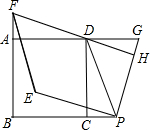 如图已知,四边形ABCD是正方形,点P与点G分别在线段BC与线段AD的延长线上,PD=PG,DF⊥PG于点H,交直线AB于点F,将线段PG绕点P逆时针旋转90°得到线段PE,连接EF.
如图已知,四边形ABCD是正方形,点P与点G分别在线段BC与线段AD的延长线上,PD=PG,DF⊥PG于点H,交直线AB于点F,将线段PG绕点P逆时针旋转90°得到线段PE,连接EF.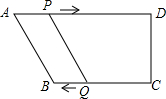 如图,在四边形ABCD中,AD∥BC,且AD>BC,BC=6cm,P、Q分别从A、C同时出发,P以1cm/s的速度由A向D运动,Q以2cm/s的速度由C向B运动,问几秒时,四边形ABQP是平行四边形?
如图,在四边形ABCD中,AD∥BC,且AD>BC,BC=6cm,P、Q分别从A、C同时出发,P以1cm/s的速度由A向D运动,Q以2cm/s的速度由C向B运动,问几秒时,四边形ABQP是平行四边形?