题目内容
 长为于12,宽为a的矩形纸片(6<a<12),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第1次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称第2次操作);若在第三次操作后,剩下的矩形为正方形,则a的值为
长为于12,宽为a的矩形纸片(6<a<12),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第1次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称第2次操作);若在第三次操作后,剩下的矩形为正方形,则a的值为考点:图形的剪拼
专题:
分析:首先根据题意可得可知当6<a<12时,第一次操作后剩下的矩形的长为a,宽为12-a,第二次操作时正方形的边长为12-a,第二次操作以后剩下的矩形的两边分别为12-a,2a-12.然后分别从12-a>2a-12与12-a<2a-12去分析求解,即可求得答案.
解答:解:由题意,可知当6<a<12时,第一次操作后剩下的矩形的长为a,宽为12-a,
所以第二次操作时剪下正方形的边长为12-a,第二次操作以后剩下的矩形的两边分别为12-a,2a-12.
此时,分两种情况:
①如果12-a>2a-12,即a<8,那么第三次操作时正方形的边长为2a-12.
则2a-12=(12-a)-(2a-12),解得a=
;
②如果12-a<2a-12,即a>8,那么第三次操作时正方形的边长为12-a.
则12-a=(2a-12)-(12-a),解得a=9.
∴第三次操作后a的值为
或9.
故答案为:
或9.
所以第二次操作时剪下正方形的边长为12-a,第二次操作以后剩下的矩形的两边分别为12-a,2a-12.
此时,分两种情况:
①如果12-a>2a-12,即a<8,那么第三次操作时正方形的边长为2a-12.
则2a-12=(12-a)-(2a-12),解得a=
| 36 |
| 5 |
②如果12-a<2a-12,即a>8,那么第三次操作时正方形的边长为12-a.
则12-a=(2a-12)-(12-a),解得a=9.
∴第三次操作后a的值为
| 36 |
| 5 |
故答案为:
| 36 |
| 5 |
点评:此题考查了折叠的性质、正方形的性质、矩形的性质.此题难度较大,注意掌握数形结合思想、分类讨论思想与方程思想的应用,注意折叠中的对应关系.

练习册系列答案
相关题目
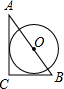 已知Rt△ABC中,∠C=90°,BC=a,AC=b,斜边AB上一点O为圆心,作⊙O使⊙O与直角边AC、BC都相切,则⊙O的半径r为( )
已知Rt△ABC中,∠C=90°,BC=a,AC=b,斜边AB上一点O为圆心,作⊙O使⊙O与直角边AC、BC都相切,则⊙O的半径r为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,在①AB=CD;②AD=CB;③EF分别是AB、CD的中点;④DE=BF这四个命题,选取三个作为条件,能否得出下列结论,并说明理由.
如图,在①AB=CD;②AD=CB;③EF分别是AB、CD的中点;④DE=BF这四个命题,选取三个作为条件,能否得出下列结论,并说明理由.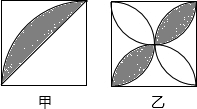 如图(甲)、(乙)是两个边长相等的正方形,甲图以边为半径在正方形内画圆弧,连接对角线;乙图以各边为直径在正方形内画半圆,阴影部分的面积分别记为S甲、S乙,那么S甲和S乙的大小关系是:S甲
如图(甲)、(乙)是两个边长相等的正方形,甲图以边为半径在正方形内画圆弧,连接对角线;乙图以各边为直径在正方形内画半圆,阴影部分的面积分别记为S甲、S乙,那么S甲和S乙的大小关系是:S甲