题目内容
6.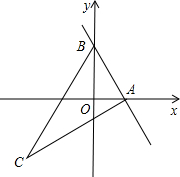 已知:如图,直线y=kx+2与x轴正半轴相交于A(t,0),与y轴相交于点B,抛物线y=-x2+bx+c经过点A和点B,点C在第三象象限内,且AC⊥AB,tan∠ACB=$\frac{1}{2}$.
已知:如图,直线y=kx+2与x轴正半轴相交于A(t,0),与y轴相交于点B,抛物线y=-x2+bx+c经过点A和点B,点C在第三象象限内,且AC⊥AB,tan∠ACB=$\frac{1}{2}$.(1)当t=1时,求抛物线的表达式;
(2)试用含t的代数式表示点C的坐标;
(3)如果点C在这条抛物线的对称轴上,求t的值.
分析 (1)把点A(1,0),B(0,2)分别代入抛物线的表达式,解方程组即可;
(2)如图:作CH⊥x轴,垂足为点H,根据△AOB∽△CHA,得到$\frac{OA}{CH}$=$\frac{OB}{AH}$=$\frac{AB}{AC}$,根据tan∠ACB=$\frac{AB}{AC}$=$\frac{1}{2}$,得到$\frac{OA}{CH}$=$\frac{OB}{AH}$=$\frac{1}{2}$,根据OA=t,得到点C的坐标为(t-4,-2t).
(3)根据点C(t-4,-2t)在抛物线y=-x2+bx+c的对称轴上,得到t-4=$\frac{b}{2}$,即b=2t-8,把点A(t,0)、B(0,2)代入抛物线的表达式,得-t2+bt+2=0,可知t2+(2t-8)t+2=0,即t2-8t+2=0,据此即可求出t的值.
解答 解:(1)∵t=1,y=kx+2,
∴A(1,0),B(0,2),
把点A(1,0),B(0,2)分别代入抛物线的表达式,得$\left\{\begin{array}{l}-1-b-c=0\\ c=2\end{array}\right.$,
解得,$\left\{\begin{array}{l}b=-1\\ c=2\end{array}\right.$,
∴所求抛物线的表达式为y=-x2-x+2.
(2)如图:作CH⊥x轴,垂足为点H,得∠AHC=∠AOB=90°,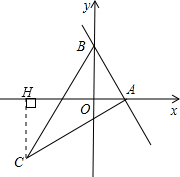
∵AC⊥AB,
∴∠OAB+∠CAH=90°,
又∵∠CAH+∠ACH=90°,
∴∠OAB=∠ACH,
∴△AOB∽△CHA,
∴$\frac{OA}{CH}$=$\frac{OB}{AH}$=$\frac{AB}{AC}$,
∵tan∠ACB=$\frac{AB}{AC}$=$\frac{1}{2}$,
∴$\frac{OA}{CH}$=$\frac{OB}{AH}$=$\frac{1}{2}$,
∵OA=t,OB=2,
∴CH=2t,AH=4,
∴点C的坐标为(t-4,-2t).
(3)∵点C(t-4,-2t)在抛物线y=-x2+bx+c的对称轴上,
∴t-4=$\frac{b}{2}$,即b=2t-8,
把点A(t,0)、B(0,2)代入抛物线的表达式,得-t2+bt+2=0,
∴-t2+(2t-8)t+2=0,即t2-8t+2=0,
解得t=4+$\sqrt{14}$,
∵点C(t-4,-2t)在第三象限,
∴t=4+$\sqrt{14}$不符合题意,舍去,
∴t=4-$\sqrt{14}$.
点评 本题考查了二次函数综合题,涉及三角函数、待定系数法求二次函数解析式、相似三角形的性质等知识,难度较大.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| 序号 | 1 | 2 | 3 | … |
| 图形 |  |  |  | … |
| ●的个数 | 8 | 16 | 24 | … |
| ☆的个数 | 1 | 4 | 9 | … |
(2)试求第6个图形中“●”的个数和“☆”的个数?
(3)试求第n个图形中“●”的个数和“☆”的个数?
 如图是每个面上都有一个汉字的正方体的一种侧面展开图,那么在原正方体的表面上,与汉字“美”相对的面上的汉字是( )
如图是每个面上都有一个汉字的正方体的一种侧面展开图,那么在原正方体的表面上,与汉字“美”相对的面上的汉字是( )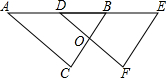 如图,△DEF是由△ABC经过平移得到的,若∠E=70°,∠A=33°,则∠ABC的度数是70°.
如图,△DEF是由△ABC经过平移得到的,若∠E=70°,∠A=33°,则∠ABC的度数是70°.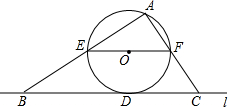 如图,直线L与⊙O相切于点D.过圆心O作EF∥L交⊙O于E、F两点,点A是⊙O上一点,连接AE、AF.并分别延长交直线L于 B、C两点.
如图,直线L与⊙O相切于点D.过圆心O作EF∥L交⊙O于E、F两点,点A是⊙O上一点,连接AE、AF.并分别延长交直线L于 B、C两点.