题目内容
19.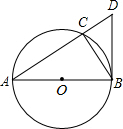 如图,⊙O是△ABC的外接圆,圆心O在AB上,过点B作⊙O的切线交AC的延长线于点D.
如图,⊙O是△ABC的外接圆,圆心O在AB上,过点B作⊙O的切线交AC的延长线于点D.(1)求证:BD2=DC•AD
(2)若AC=8cm,DC=2cm,求⊙O的面积.
分析 (1)先根据圆周角定理得出∠ACB=90°,再由切线的性质得出∠ABD=90°,进而可得出△BCD∽△ABD,据此可得出结论;
(2)先根据(1)中的结论得出BD2的值,再由勾股定理求出AB的长,由圆的面积公式即可得出结论.
解答 解:(1)∵AB是⊙O的直径,
∴∠ACB=90°.
∵BD是⊙O的切线,
∴∠ABD=90°,
∴△BCD∽△ABD,
∴$\frac{BD}{AD}$=$\frac{DC}{BD}$,即BD2=DC•AD;
(2)∵AC=8cm,DC=2cm,
∴AD=8+2=10cm.
∵BD2=DC•AD,
∴BD2=2×10=20.
∵∠ABD=90°,
∴AB=$\sqrt{A{D}^{2}-B{D}^{2}}$=$\sqrt{100-20}$=4$\sqrt{5}$,
∴OA=$\frac{1}{2}$AB=2$\sqrt{5}$,
∴⊙O的面积=π×(2$\sqrt{5}$)2=20π.
点评 本题考查的是相似三角形的判定和性质及圆的切线的性质,利用切线的性质得到角之间的关系是解题的关键.

练习册系列答案
相关题目
14.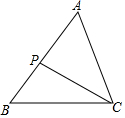 如图,在△ABC中,P是边AB上一点,连结CP,下面条件中能使△ACP∽△ABC的条件有( )个.
如图,在△ABC中,P是边AB上一点,连结CP,下面条件中能使△ACP∽△ABC的条件有( )个.
①∠ACP=∠B
②∠APC=∠ACB
③AC2=AP•AB
④CP平分∠ACB.
 如图,在△ABC中,P是边AB上一点,连结CP,下面条件中能使△ACP∽△ABC的条件有( )个.
如图,在△ABC中,P是边AB上一点,连结CP,下面条件中能使△ACP∽△ABC的条件有( )个.①∠ACP=∠B
②∠APC=∠ACB
③AC2=AP•AB
④CP平分∠ACB.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.如果抛物线y=(m-1)x2的开口向上,那么m的取值范围是( )
| A. | m>1 | B. | m≥1 | C. | m<1 | D. | m≤1 |
 如图,在△ABC中,∠B=30°,∠C=60°,AD是高,AE是角平分线,求∠EAD的度数.
如图,在△ABC中,∠B=30°,∠C=60°,AD是高,AE是角平分线,求∠EAD的度数. 如图,将长方形纸片ABCD沿其对角线AC折叠,使点B落在点B′的位置,AB′与CD交于点E.
如图,将长方形纸片ABCD沿其对角线AC折叠,使点B落在点B′的位置,AB′与CD交于点E.