题目内容
11. 如图,将长方形纸片ABCD沿其对角线AC折叠,使点B落在点B′的位置,AB′与CD交于点E.
如图,将长方形纸片ABCD沿其对角线AC折叠,使点B落在点B′的位置,AB′与CD交于点E.(1)求证:△AED≌△CEB′;
(2)求证:点E在线段AC的垂直平分线上;
(3)若AB=8,AD=3,求图中阴影部分的周长22(直接写出答案)
(4)求EB'的长度,并写出解题过程.
分析 (1)由四边形ABCD为矩形及折叠的特性,得到B′C=BC=AD,∠B′=∠B=∠D=90°,∠B′EC=∠DEA,得到△AED≌△CEB′.
(2))由△AED≌△CEB′,得出EA=EC,所以点E在线段AC的垂直平分线上
(3)阴影部分的周长为AD+DE+EA+EB′+B′C+EC,即矩形的周长;
(4)设B′E=x,则DE=x,CE=CD-x,根据勾股定理即可得到结论.
解答 (1)证明:∵四边形ABCD为矩形,
∴B′C=BC=AD,∠B′=∠B=∠D=90°
∵∠B′EC=∠DEA,
在△AED和△CEB′中,$\left\{\begin{array}{l}{∠B′ED=∠DEA}\\{∠B′=∠D}\\{B′C=AD}\end{array}\right.$,
∴△AED≌△CEB′(AAS);
(2)∵△AED≌△CEB′,
∴EA=EC,
∴点E在线段AC的垂直平分线上;
(3)∵△AED≌△CEB′,
∴AE=CE,DE=EB′,
∵将长方形纸片ABCD沿其对角线AC折叠,使点B落在点B′的位置,
∴CB′=BC=AD,
∴阴影部分的周长为AD+DE+EA+EB′+B′C+EC,
=AD+DE+EC+EA+EB′+B′C,
=AD+DC+AB′+B′C,
=3+8+8+3
=22;
故答案为:22;
(4)设B′E=x,
则DE=x,CE=CD-x,
∵B′C2+B′E2=CE2,
∴32+x2=(8-x)2,
∴x=$\frac{55}{16}$,
∴EB′=$\frac{55}{16}$.
点评 本题主要考查了图形的折叠问题,全等三角形的判定和性质,及矩形的性质,勾股定理.熟记翻折前后两个图形能够重合找出相等的角是解题的关键.

练习册系列答案
相关题目
2.尼罗河发源于维多利亚西群山,全长6670000米,其长度用科学记数法可表示为( )
| A. | 6.67×105 | B. | 0.667×107 | C. | 6.67×106 | D. | 66.7×106 |
6.雾霾天气严重影响市民的生活质量,在今年元旦期间,某校七年级一班的同学对“雾霾天气的主要成因”就市民的看法做了随机调查,并对调查结果进行了整理,绘制了不完整的统计图表(如下图),观察分析并回答下列问题.
(1)本次被调查的市民共有200人;
(2)补全条形统计图;
(3)图2中区域B所对应的扇形圆心角为108度.

| 组别 | 雾霾天气的主要成因 | 百分比 |
| A | 工业污染 | 45% |
| B | 汽车尾气排放 | m |
| C | 炉烟气排放 | 15% |
| D | 其它(滥砍滥伐等) | n |
(2)补全条形统计图;
(3)图2中区域B所对应的扇形圆心角为108度.

16.在1,0,-1,-2这四个数中,最小的数是( )
| A. | -1 | B. | -2 | C. | 0 | D. | 1 |
 按下列要求画出图形(在原图上画)如图,平面上有三点A,B,C
按下列要求画出图形(在原图上画)如图,平面上有三点A,B,C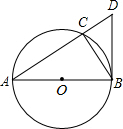 如图,⊙O是△ABC的外接圆,圆心O在AB上,过点B作⊙O的切线交AC的延长线于点D.
如图,⊙O是△ABC的外接圆,圆心O在AB上,过点B作⊙O的切线交AC的延长线于点D.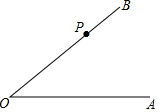 如图,P是∠AOB的边OB上一点.
如图,P是∠AOB的边OB上一点. 如图,OC平分∠AOB,若∠AOC=27°30′,则∠AOB=55度.
如图,OC平分∠AOB,若∠AOC=27°30′,则∠AOB=55度.