题目内容
11．
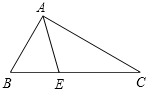如图，在△ABC中，已知∠B=60°，∠C=30°，AE是△ABC角平分线，求：∠BEA的度数．
分析 先根据三角形内角和定理求出∠BAC的度数，再由角平分线的性质得出∠CAE的度数，由三角形外角的性质即可得出结论．
解答 解：∵在△ABC中，∠B=60°，∠C=30°，
∴∠BAC=180°-60°-30°=90°．
∵AE是△ABC角平分线，
∴∠CAE=$\frac{1}{2}$∠BAC=45°，
∴∠BEA=∠C+∠CAE=30°+45°=75°．
点评 本题考查的是三角形内角和定理，熟知三角形内角和是180°是解答此题的关键．
练习册系列答案
浙江之星课时优化作业系列答案
激活思维优加课堂系列答案
相关题目
1．表是二次函数y=ax2+bx+c的部分x，y的对应值：
（1）二次函数图象的开口向上，顶点坐标是（1，-2），m的值为2；
（2）当x＞0时，y的取值范围是y≥-2；
（3）当抛物线y=ax2+bx+c的顶点在直线y=x+n的下方时，n的取值范围是n＞-3．
| x | … | -1 | -$\frac{1}{2}$ | 0 | $\frac{1}{2}$ | 1 | $\frac{3}{2}$ | 2 | $\frac{5}{2}$ | 3 | … |
| y | … | m | $\frac{1}{4}$ | -1 | $-\frac{7}{4}$ | -2 | $-\frac{7}{4}$ | -1 | $\frac{1}{4}$ | 2 | … |
（2）当x＞0时，y的取值范围是y≥-2；
（3）当抛物线y=ax2+bx+c的顶点在直线y=x+n的下方时，n的取值范围是n＞-3．
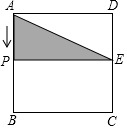正方形ABCD的边长为4cm，点E是CD的中点，有一动点P由A出发沿B、C、D方向以2cm/秒的速度匀速运动，直至回到A点停止，设点P运动时间为t秒，当S△AEP=3cm2时，t的值为$\frac{3}{4}$或$\frac{17}{4}$或$\frac{23}{4}$或$\frac{13}{4}$．
如图所示，△ABC中，DE∥FG∥BC，且AD=DF=FB，则S△AFG：S△ABC=4：9．